Algebra Tricks – 4

Q. (1)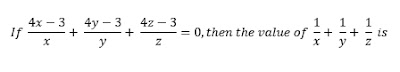 

(A) 3                (B) 4                 (C) 6                   (D) 9

Although this equation is symmetrical, and hence we can assume x = y = z to solve it. But you should know one more thing about such equations. If the sum of certain number of terms is zero, you can assume each term to be zero. That means,

(4x – 3)/x = 0 or x = 3/4

(4y – 3)/y = 0 or y = 3/4

(4z – 3)/z = 0 or z = 3/4

So, 1/x + 1/y + 1/z = 4

Answer: (B)

1. (2) If x^2 = y + z, y^2 = z + x, z^2 = x + y, then find the value of 

 

(A) 1                (B) 2                 (C) 0                   (D) -1

Symmetrical equation, hence x = y = z

x^2 = x + x

x^2 = 2x

x = 2

Hence x = y = z = 2

Put in the expression

= 1/3 + 1/3 + 1/3

= 1

Answer: (A)

1. (3)

This is a very famous question-type. In such questions we take everything on RHS to LHS and then try to make squares. You will get,

(x – 1)^2 + (y + 1)^2 + (z + 1)^2 = 0

And like I said before, if the sum of certain number of terms is zero, we can assume each term to be zero.

(x – 1)^2 = 0, (y + 1)^2 = 0, (z + 1)^2 = 0

Hence, x = 1, y = -1 and z = -1

Put these values in (2x – 3y + 4z)

= 2(1) -3(-1) + 4(-1)

= 1

Answer: (D)

1. (4)

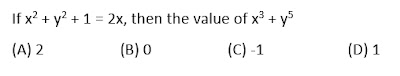
Take everything to LHS,

(x – 1)^2 + y^2 = 0

Hence, x = 1 and y = 0

Put these values in the expression

= (1)^3 + 0^5

= 1

Answer: (D) 

1. (5)

               (A) 5/12                    (B) 12/5                     (C) 5/7                    (D) 7/5

By Componendo and Dividendo, whenever you see any equation written in the form

(m + n)/(m – n) = p

You can directly write m/n = (p + 1)/(p – 1)

In this question

m = √(3 + x), n = √(3 – x), p = 2

Hence, by Componendo-Dividendo

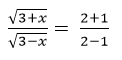
Squaring both sides

(3 + x)/(3 – x) = 9

Again apply componendo-dividendo

3/x = (9 + 1)/(9 – 1)

3/x = 5/4

x = 12/5

Answer: (B)

1. (6) If x = 332, y = 333, z = 335, then the value of x^3 + y^3 + z^3 – 3xyz is

(A) 10000             (B) 7000              (C) 9000               (D) 8000

There is one more formula for a^3 + b^3 + c^3 – 3abc, apart from the one which you know

Hence,

x^3 + y^3 + z^3 – 3xyz = 1/2(332 + 333 + 335)[(332 – 333)^2 + (333 – 335)^2 + (335 – 332)^2]

= 1/2 (1000)[1 + 4 + 9]

= 7000

Answer: (B)

1. 7)

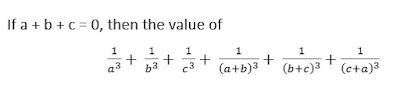
(A) -1                 (B) 3abc                   (C) 1                      (D) 0

a + b + c = 0 is symmetrical

Whenever any symmetrical equation is equal to zero, and the expression whose value is asked, is also symmetrical( and the numerator of the terms is also 1), then the value of that expression will also be zero.

Answer: (D)

1. (8)

(A) -2                (B) -1/2                   (C) 0                   (D) 1/2

Same logic

Value of the expression = 0

Answer: (C)

1. (9)

                             (A) 9            (B) 0                (C) 8                (D)

Although a + b + c = 0, is a symmetrical equation, and the expression ((a+b)/c+ (b+c)/a+ (c+a)/b)(a/(b+c)+ b/(c+a)+c/(a+b)) is also symmetrical. But the numerator of the terms is not 1. Hence we can’t say that the answer is zero.

We will solve it by assuming a=b=c. Hence

= (2 + 2 + 2)(1/2 + 1/2 + 1/2)

= 6 * 3/2

= 9

Answer: (A)

1. (10)

ab + bc + ca = 0 is symmetrical

Hence value of the expression = 0

Answer: (B)

If you have any doubts in this article, please drop a comment…