 For Daily Job Alert For Daily Job Alert |
Join Our Whats App Channel |
 For Free Study Material For Free Study Material |
Join Our Telegram Channel |
The time value of money functions related to calculation of Present Value (PV), Future Value (FV), etc. are important mathematical concepts related to bond market. An outline of the same with illustrations is provided below.
|
Time Value of Money Money has time value as a Rupee today is more valuable and useful than a Rupee a year later. The concept of time value of money is based on the premise that an investor prefers to receive a payment of a fixed amount of money today, rather than an equal amount in the future, all else being equal. In particular, if one receives the payment today, one can then earn interest on the money until that specified future date. Further, in an inflationary environment, a Rupee today will have greater purchasing power than after a year. Present value of a future sum The present value formula is the core formula for the time value of money. The present value (PV) formula has four variables, each of which can be solved for: Present Value (PV) is the value at time=0 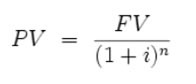 The cumulative present value of future cash flows can be calculated by adding the contributions of FVt, the value of cash flow at time=t 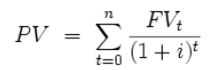 An illustration Taking the cash flows as;
Assuming that the interest rate is at 10% per annum; The discount factor for each year can be calculated as 1/(1+interest rate)^no. of years The present value can then be worked out as Amount x discount factor The PV of ₹100 accruing after 3 years:
The cumulative present value = 90.91+82.64+75.13 = ₹ 248.69 Net Present Value (NPV) Net present value (NPV) or net present worth (NPW) is defined as the present value of net cash flows. It is a standard method for using the time value of money to appraise long-term projects. Used for capital budgeting, and widely throughout economics, it measures the excess or shortfall of cash flows, in present value (PV) terms, once financing charges are met. Formula Each cash inflow/outflow is discounted back to its present value (PV). Then they are summed. Therefore 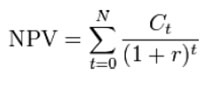 Where In the illustration given above under the Present value, if the three cash flows accrues on a deposit of ₹ 240, the NPV of the investment is equal to 248.69-240 = ₹ 8.69 |
How is the Price of a bond calculated? What is the total consideration amount of a trade and what is accrued interest?
The price of a bond is nothing but the sum of present value of all future cash flows of the bond. The interest rate used for discounting the cash flows is the Yield to Maturity (YTM) of the bond. Price can be calculated using the excel function ‘Price’ (please refer to Annex 6,).
Accrued interest is the interest calculated for the broken period from the last coupon day till a day prior to the settlement date of the trade. Since the seller of the security is holding the security for the period up to the day prior to the settlement date of the trade, he is entitled to receive the coupon for the period held. During settlement of the trade, the buyer of security will pay the accrued interest in addition to the agreed price and pays the ‘consideration amount’.
An illustration is given below;
For a trade of ₹ 5 crore (face value) of security 8.83% 2023 for settlement date Jan 30, 2014 at a price of ₹100.50, the consideration amount payable to the seller of the security is worked out below:
Here the price quoted is called ‘clean price’ as the ‘accrued interest’ component is not added to it.
Accrued interest:
The last coupon date being Nov 25, 2013, the number of days in broken period till Jan 29, 2014 (one day prior to settlement date i.e. on trade day) are 65.
| The accrued interest on ₹100 face value for 65 days | = 8.83 x (65/360) |
| = ₹1.5943 |
When we add the accrued interest component to the ‘clean price’, the resultant price is called the ‘dirty price’. In the instant case, it is 100.50+1.5943 = ₹102.0943
| The total consideration amount | = Face value of trade x dirty price |
| = 5,00,00,000 x (102.0943/100) | |
| = ₹ 5,10,47,150 |
What is the relationship between yield and price of a bond?
If market interest rate levels rise, the price of a bond falls. Conversely, if interest rates or market yields decline, the price of the bond rises. In other words, the yield of a bond is inversely related to its price. The relationship between yield to maturity and coupon rate of bond may be stated as follows:
- When the market price of the bond is less than the face value, i.e., the bond sells at a discount, YTM > > coupon yield.
- When the market price of the bond is more than its face value, i.e., the bond sells at a premium, coupon yield > > YTM.
- When the market price of the bond is equal to its face value, i.e., the bond sells at par, YTM = = coupon yield.
How is the yield of a bond calculated?
An investor who purchases a bond can expect to receive a return from one or more of the following sources:
- The coupon interest payments made by the issuer;
- Any capital gain (or capital loss) when the bond is sold/matured; and
- Income from reinvestment of the interest payments that is interest-on-interest.
The three yield measures commonly used by investors to measure the potential return from investing in a bond are briefly described below:
i) Coupon Yield
The coupon yield is simply the coupon payment as a percentage of the face value. Coupon yield refers to nominal interest payable on a fixed income security like G-Sec. This is the fixed return the Government (i.e., the issuer) commits to pay to the investor. Coupon yield thus does not reflect the impact of interest rate movement and inflation on the nominal interest that the Government pays.
Coupon yield = Coupon Payment / Face Value
Illustration:
Coupon: 8.24
Face Value: ₹100
Market Value: ₹103.00
Coupon yield = 8.24/100 = 8.24%
ii) Current Yield
The current yield is simply the coupon payment as a percentage of the bond’s purchase price; in other words, it is the return a holder of the bond gets against its purchase price which may be more or less than the face value or the par value. The current yield does not take into account the reinvestment of the interest income received periodically.
Current yield = (Annual coupon rate / Purchase price)X100
Illustration:
The current yield for a 10 year 8.24% coupon bond selling for ₹103.00 per ₹100 par value is calculated below:
Annual coupon interest = 8.24% x ₹100 = ₹8.24
Current yield = (8.24/103) X 100 = 8.00%
The current yield considers only the coupon interest and ignores other sources of return that will affect an investor’s return.
iii) Yield to Maturity
Yield to Maturity (YTM) is the expected rate of return on a bond if it is held until its maturity. The price of a bond is simply the sum of the present values of all its remaining cash flows. Present value is calculated by discounting each cash flow at a rate; this rate is the YTM. Thus YTM is the discount rate which equates the present value of the future cash flows from a bond to its current market price. In other words, it is the internal rate of return on the bond. The calculation of YTM involves a trial-and-error procedure. A calculator or software can be used to obtain a bond’s YTM easily.
|
YTM Calculation YTM could be calculated manually as well as using functions in any standard spread sheet like MS Excel. Manual (Trial and Error) Method Manual or trial and error method is complicated because G-Secs have many cash flows running into future. This is explained by taking an example below. Take a two year security bearing a coupon of 8% and a price of say ₹ 102 per face value of ₹ 100; the YTM could be calculated by solving for ‘r’ below. Typically it involves trial and error by taking a value for ‘r’ and solving the equation and if the right hand side is more than 102, take a higher value of ‘r’ and solve again. Linear interpolation technique may also be used to find out exact ‘r’ once we have two ‘r’ values so that the price value is more than 102 for one and less than 102 for the other value.
Spread Sheet Method using MS Excel In the MS Excel programme, the following function could be used for calculating the yield of periodically coupon paying securities, given the price. YIELD (settlement,maturity,rate,price,redemption,frequency,basis) Wherein; Settlement is the security’s settlement date. The security settlement date is the date on which the security and funds are exchanged. Maturity is the security’s maturity date. The maturity date is the date when the security expires. Rate is the security’s annual coupon rate. Price is the security’s price per ₹100 face value. Redemption is the security’s redemption value per ₹100 face value. Frequency is the number of coupon payments per year. (2 for Government bonds in India) Basis is the type of day count basis to use. (4 for Government bonds in India which uses 30/360 basis) |
What are the day count conventions used in calculating bond yields?
Day count convention refers to the method used for arriving at the holding period (number of days) of a bond to calculate the accrued interest. As the use of different day count conventions can result in different accrued interest amounts, it is appropriate that all the participants in the market follow a uniform day count convention.
For example, the conventions followed in Indian market are given below.
Bond market: The day count convention followed is 30/360, which means that irrespective of the actual number of days in a month, the number of days in a month is taken as 30 and the number of days in a year is taken as 360.
Money market: The day count convention followed is actual/365, which means that the actual number of days in a month is taken for number of days (numerator) whereas the number of days in a year is taken as 365 days. Hence, in the case of T-Bills, which are essentially money market instruments, money market convention is followed.
In some countries, participants use actual/actual, some countries use actual/360 while some use 30/actual. Hence the convention changes in different countries and in different markets within the same country (eg. Money market convention is different than the bond market convention in India).









