Geometry Notes on Quadrilateral Tips and Tricks
In this article we will discuss about the quadrilateral which is an important topic of Geometry. This topic is useful both in Geometry and Mensuration. Here we cover all the quadrilateral and various properties and theorem related to them.
Quadrilateral:
A plane figure bounded by four line segment is called the quadrilateral. The area enclosed by the four side must not be zero.
A simple quadrilateral has four sides and four angle.
Sum of the angle of quadrilateral is always 360°
∠A+∠B+∠C+∠D=360°
Area of quadrilateral ABCD = 1/2[AC(DE+BF)]
DE and BF are the perpendicular on diagonal AC.
Types of Quadrilateral
Parallelogram:
- A quadrilateral whose opposite sides are equal and parallel
- Opposite sides angle are equal(∠A=∠C)and (∠B=∠D).
- Sum of any adjacent angle is 180°
- Diagonals bisect each other.
- Diagonals need not be perpendicular or equal.
- Each diagonals divides a parallelogram into two triangle ofequal area.
- Area of parallelogram is double the area of the triangle formed by diagonals.
- Bisectors of the angle of a parallelogram form a rectangle.
- A parallelogram inscribed inside a circle is rectangle.
- A parallelogram circumscribed about a circle is a rhombus.
- AC2+BD2=AB2+BC2+CD2+AD2=2(AB2+BC2)
- Area of parallelogram ABCD= Base *Height
- A parallelogram is a rectangle if its diagonal are equal.
- Parallelogram that lie on the same base and between the same parallel lines are equal in area.
area of Parallelogram ABCD=Area of Parallelogram ABPQ
- If a triangle and a parallelogram are on same base and between the same parallel lines , then area of triangle is half of parallelogram.
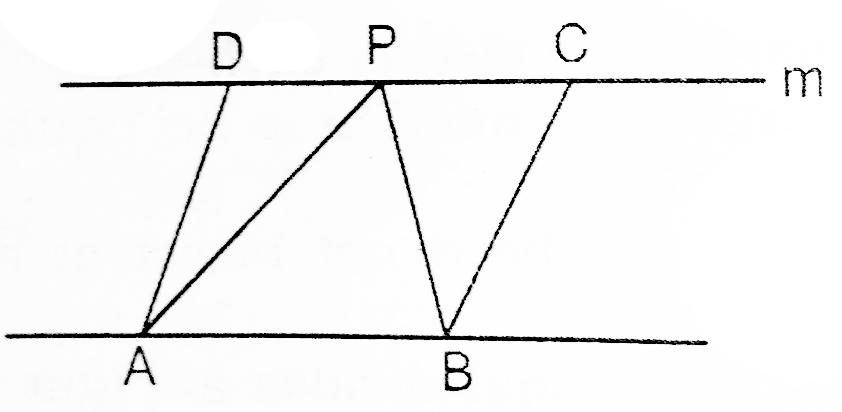
Area of triangle APB=1/2(area of parallelogram ABCD)
Rectangles:
- A rectangle is a parallelogram whose all angles 90°.
- Diagonal are equal and bisect each other but not necessarily at 90°.
- A square has maximum area for a given perimeter of rectangles.
- Figures formed by joining the mid points of the adjacent side of the rectangle is a rhombus.
- Angle Bisectors of a rectangle form another rectangle.
- Area of rectangle=length*breadth
- Diagonals of the rectnagle[AC=BD=√(l2+b2)]
Square:
- A square is a rectangle with all its side equal and all the angle equal to 90°.
- Diagonals are equal and bisect each other at 90°
- Figure formed by joining the midpoint of the sides of square is a square.
- Area= a2
- Diagonal=√2*a
Rhombus:
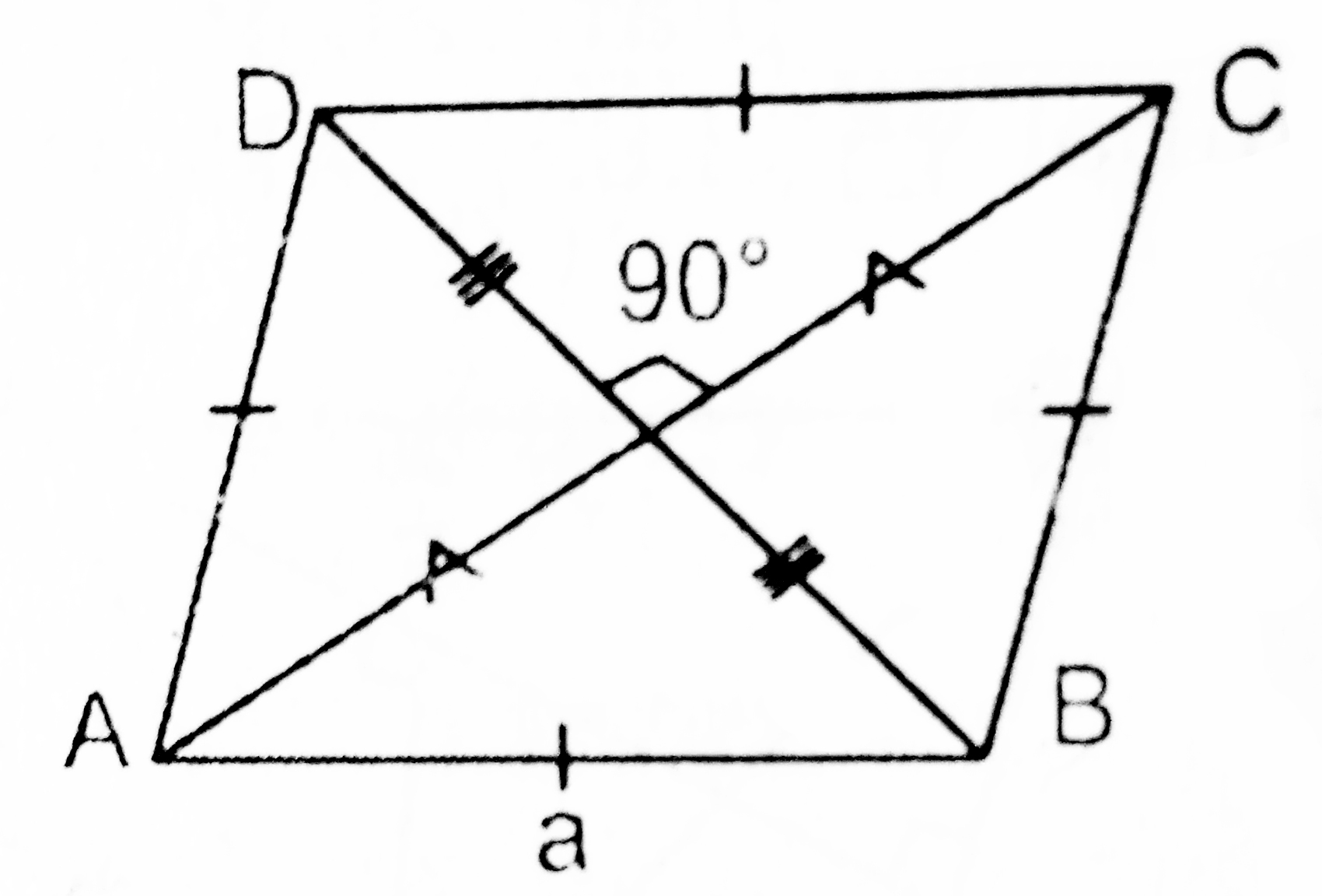
- A parallelogram having all its sides equal is a rhombus.
- Diagonals of the rhombus bisect each other at right angle but they are not necessarily equal.
- A rhombus may or may not be a square but all the square are rhombus.
- Figure formed by joining the midpoint of the adjacent sides of a rhombus is a rectangle.
- A parallelogram is a rhombus if its diagonals are perpendicular to each other.
- Area of rhombus=1/2(product of diagonal)
- here AC and BD are diagonal.
- AC2+BD2=4AB2
Trapezium:
- A quadrilateral is a trapezium with only two sides parallel to each other.
- sum of opposite angle equal to 180(∠A+∠C=∠B+∠D=180°)
- Area of trapezium =1/2[(sum of parallel sides)*heights]
= 1/2[(AB+CD)*DM]
- sum of the square of diagonal =(sum of square of non parallel sides) +2(products of parallel sides)
AC2+BD2=BC2+AD2+2AB*CD
- If E and F are the midpoints of two non-parallel sides AD and BC respectively then
EF=1/2(AB+BC) 
- AO*OD=OC*BO
- E and F are the mid-points of the side AB and AC respectively then,
EF=1/2(BC) and EF parllel BC
Polygon:
- A closed figure bounded by three or more than three straight lines.
Convex Polygon:
- A polygon in which none of its interior angle is more than 180°.
Concave Polygon:
- A polygon in which at-least one of its interior angle is more than 180°
Regular Polygon:
- A polygon in which all the sides are equal and also the interior angles are equal is called a regular polygon.
- if n is the total no sides of the polygon then
- Sum of its interior angle is (n-2)*180°
- Each exterior angle=360°/n
- Sum of all exterior angle is 360°
- Sum of interior angle and exterior angle is 180°
- Number of diagonals =n(n-3)/2
