For Daily Job Alert For Daily Job Alert |
Join Our Whats App Channel |
 For Free Study Material For Free Study Material |
Join Our Telegram Channel |
Triangles and their Properties Tips and Tricks
Today we will be covering a very important topic from the Advance Maths part of the Quantitative Aptitude section that is – Important notes on Triangles and their Properties.
Triangles and their properties
Area of triangle

- When base and corresponding height is known: ½ * base * height = ½*c*h
- When all sides are given (Heron’s formulae): {s (s – a) (s – b) (s – c)}1/2 where, s = (a+b+c)/2
- When two sides and corresponding angle is given.: ½ a*c*sinθ
- When all the median are given (Median is a line joining the vertex to the opposite side at midpoint): 4/3 * {s(s – m1) (s – m2) (s –m3)}1/2
Note: Where, s = (m1+m2+m3)/2, m1,m2,m3 are three medians of the Triangle.
- When all the heights are given: 1/Area of ∆ = 4 {G (G – 1/h1) (G – 1/h2) (G – 1/h3),
Note: Where, G = ½ (1/h1 + 1/h2 + 1/h3)
Sine formulae of triangle
a/SinA = b/sinB = c/SinC = 2R Where, R is Circumradius
Cosine Formulae of triangle
CosA = b2 +c2 – a2 / 2bc
CosB= a2 +c2 – b2 / 2ac
CosC = b2 +a2 – c2 / 2ba
An interesting result based of cosine formulae
If in a triangle CosA = b2 +c2 – a2 / 2bc, Whereas b & c are the smaller sides then
Case I, b2 +c2 is greater than a2 then angle A is acute.
Case II, b2 +c2 is smaller than a2 then angle A is obtuse.
Case III, b2 +c2 is equals to a2 then angle A is Right Angle.
For example,
Ques: Find the type of the triangle ABC whose 3 sides are of length 11, 3 & 9.
Solution: Sum of square of two smaller sides is 32 + 92 = 9 + 81 = 90
Square of largest side is 112 = 121.
Hence, this triangle is obtuse angled triangle.
TRIANGLES AND ITS CERVICES
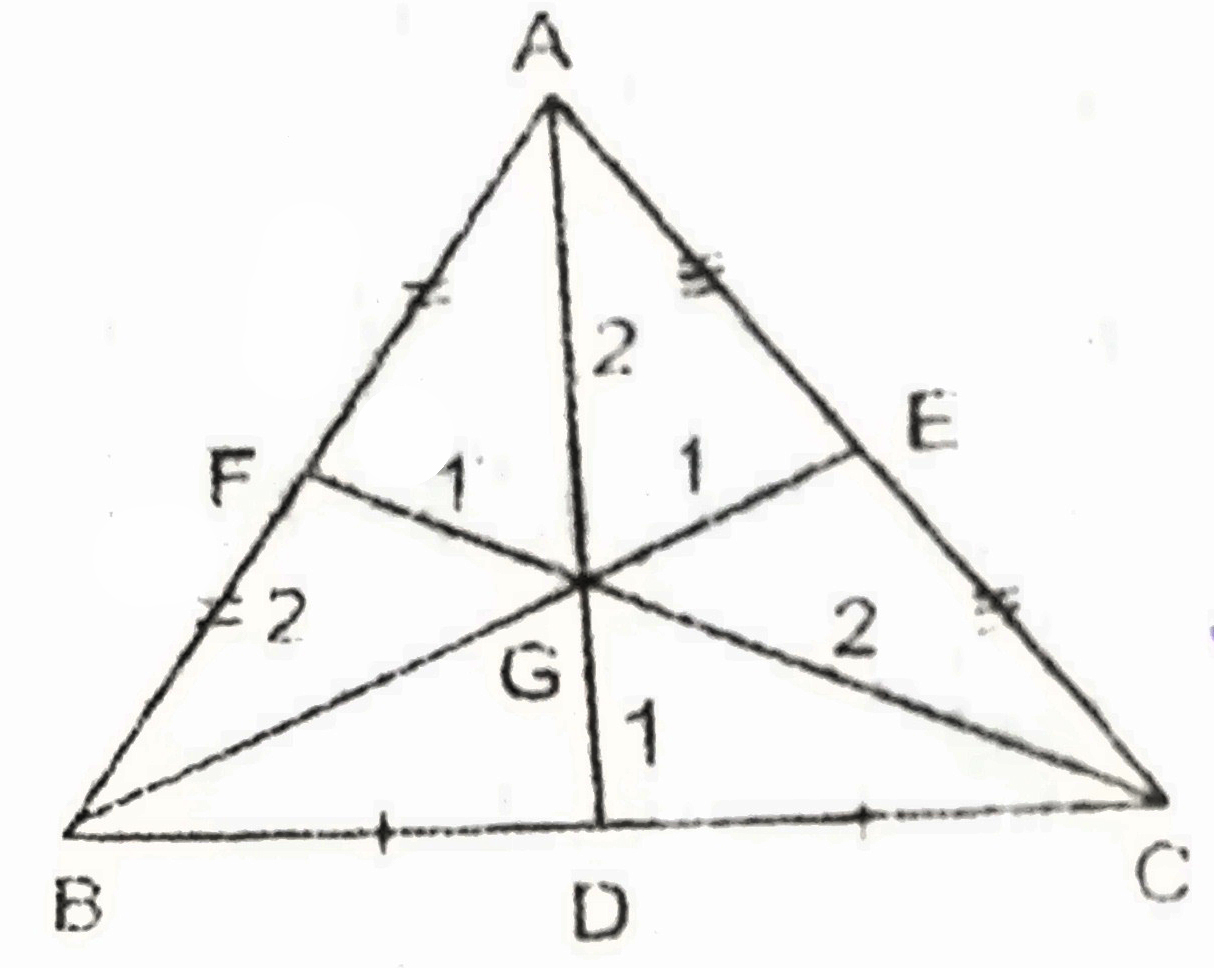
Medians of a Triangle

The medians of a triangle are line segments joining each vertex to the midpoint of the opposite side. The medians always intersect in a single point, called the centroid.
In the adjoining figure D, E, & F are midpoints of the side of the triangle while Line Segment AD, BE & CF are median. They are meeting at a common point I which is the centroid.
Properties:
- Centroid divides the Median in the ratio 2:1. i.e AI/ID = 2/1
- Apollonius Theoram:- To find the length of median when all sides are given: 4 * AD2 = 2(AC2 + AB2) – BC2
- All 3 median of a triangle divides the triangle in 6 equal parts.
i.e. ar of ∆AFI = ar of ∆AEI = ar of ∆BFI = ar of ∆BDI= ar of ∆CDI= ar of ∆CEI= ar of ∆ABC/6
Angle Bisectors

Angle bisectors are the line segment which bisects the internal angles of the triangle. All the three angle bisectors meet at a common point called as Incentre.
In the adjoining figure Line Segment A1T1, A2T2, & A3T3 are Angle Bisector. While point I is Incentre of the triangle.
Incentre is the only point from which we can draw a circle inside the triangle which will touch all the sides of the triangle at exactly one point & this circle has a special name known as Incircle. And the radius of this circle is known as Inradius.
Properties:
- Inradius = Area of ∆ A1A2A3 / Semi perimeter of ∆ A1A2A3
- Angle formed at the incentre by any two angle bisector: Angle A1IA3 = Angle A1A2A3 /2) + 90o
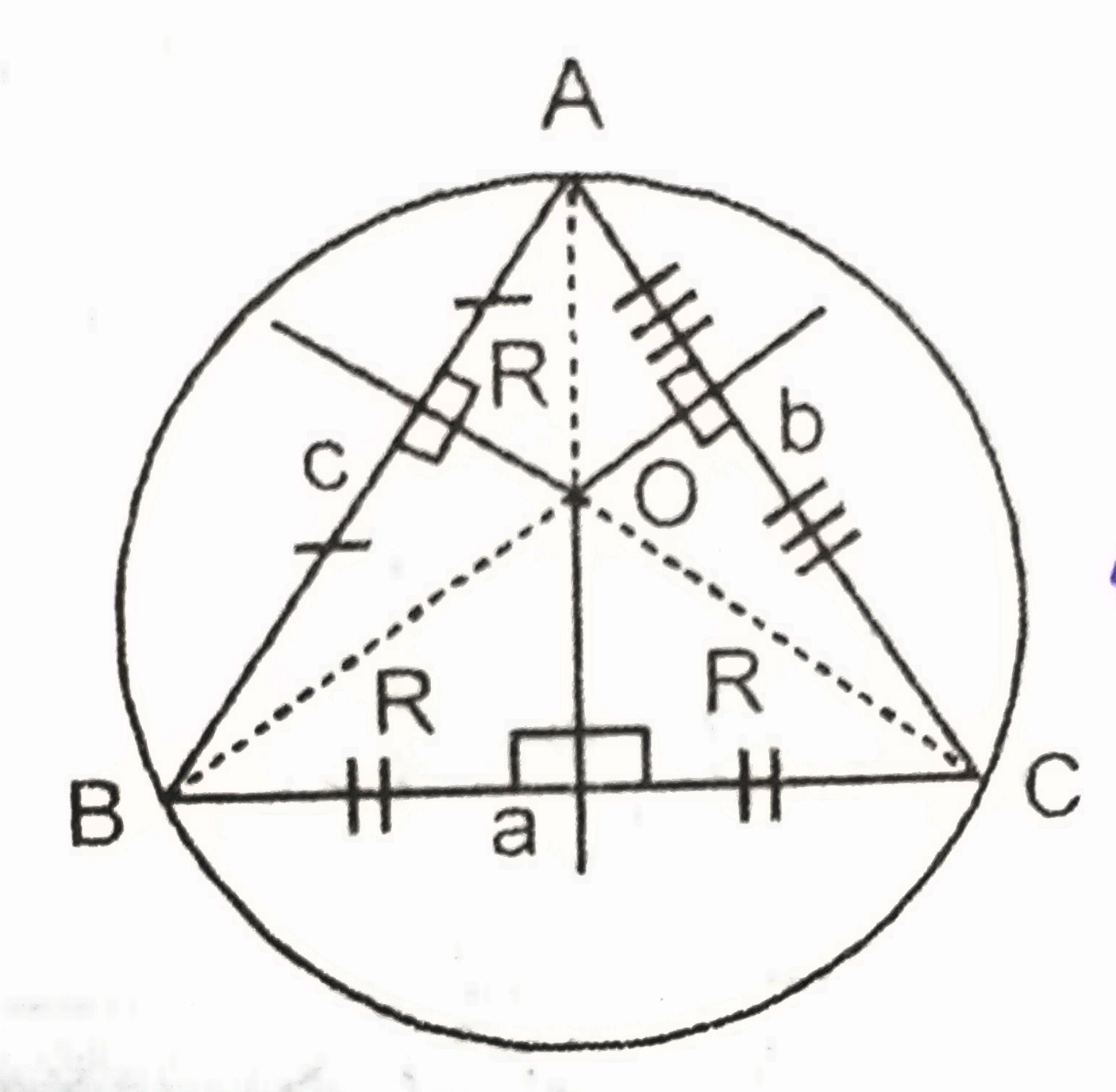
Perpendicular Bisectors of Sides of the Triangle

When the perpendicular bisectors of the side of the triangle is drawn they meet at a common point known as circumcentre.
This circumcentre is a special point as from this point we can draw a circle which will enclose the triangle in a way that all the vertex of the triangle lie on the circle. The radius of this circle is known as circumradius.
Properties:
In the adjoining figure DP, EP, & FP are perpendicular bisector of sides of the triangle. Point P is circumcentre.
- Circumradius = length of side AC * CB * BA / 4 * Area of triangle
- Angle formed at the circumcentre by any two linesegment joining circumcentre to the vertex: Angle APC = 2 * Angle ABC
Altitude of the Triangle

The orthocenter of a triangle is the point where the three altitudes meet. This point may be inside, outside, or on the triangle.
In the adjoining figure AD, BE, & CF are three altitudes of a triangle. And point O is the orthocenter.
Properties:
- Angle BOC + Angle BAC = 180o
SIMILAR TRIANGLE

If two triangles are similar, then the corresponding sides we have, shows the following relation:
- The ratio of sides of triangle is proportional to each other.
Like AB/DE = BC/EF = CA/FD
For example:
If AB = 6cm, BC = 10cm & DE = 2cm. Find EF
Solution: AB/DE = BC/EF, 6/2 = 10/EF, Therefore EF = 2*10/6 = 10/3
- The height, angle bisector, inradius & circumradius are proportional to the sides of triangle.
Median ∆ABC / Median ∆DEF = Height ∆ABC/ Height ∆DEF = AB/DE
- The areas of the triangles are proportional to the square of the sides of the corresponding triangle.
Area ∆ABC/ Area ∆DEF = (AB/DE) 2
For example:
If AB = 6cm, DE = 10cm & Area of ∆ABC is 135 sqcm. Find Area of ∆DEF.
Solution: Area ∆ABC/ Area ∆DEF = (AB/DE) 2
135/ Area ∆DEF = (6/10)2 , Area ∆DEF = 135*(5/3)2 = 375 sqcm.
In a right angled triangle, the triangles on each sides of the altitude drawn from the vertex of the right angle to the hypotenuse are similar to each other and to the parent triangle.

- ∆ ABC ≈ ∆ ABD
- ∆ ABC ≈ ∆ CBD
- ∆ DBC ≈ ∆ ABD
Proof: In ∆ ABC & ∆ ABD. Angle B and Angle D is 90o. & Angle A is common in both. Hence by AA rule Both triangles are similar.
Some Important Question are as follows::
(1)In the given figure ![]() =?
=?

(a)3600
(b) 7200
(c) 1800
(d) 3000
Ans. (a)
Here in triangle AEC
![]()
In triangle BFD
![]()
Adding (i) and (ii) we get,
![]() =360°
=360°
(2)In the given figure ![]()

(a) 9000
(b) 7200
(c) 1800
(d) 5400
Ans. (c)
In star like figure we calculate the sum of angle by using formula (n-4) 180, when n is the number of point in the star.


(3) In the given figure below, if AD = CD = BC, and ![]() =96°,How much is
=96°,How much is ![]()

(a) 320
(b) 840
(c) 640
(d) can’t be determined
Ans. (c)
Here ![]()
![]()


and from triangle ACB
![]()

(4)In the trapezium ABCD shown below, AD || BC and AB = 6, BC = 7, CD = 8, AD = 17, if sides AB and CD are extended to meet at E, find the measure of <AED

(a) 1200
(b) 1000
(c) 800
(d) 900
Ans. (d)


(5)In the given figure, ABCD is a rhombus and AR = AB = BP, then the value of <RTP is

(a) 600
(b) 900
(c) 1200
(d) 750
Ans. (b)
Let ![]()
![]()
Similarly,

( ABCD is a rhombus)

In this article we will discuss about the various centers of triangle. In SSC CGL exams 1 or 2 question generally come in exam from this chapter.
There are four centres in a triangle triangle:
- In-centre
- Circum-centre
- Centroid
- Ortho centre
In-centre:
The point of intersection of the all the three angle bisectors of a triangle is called as In-centre
The distance of the in-centre from the all the three sides is equal(ID=IE=IF=inradius “r”)
In-radius (r)= Area of triangle/Semiperimetre=A/S
∠BIC = 90 +∠A/2
∠AIC=90+∠B/2
∠AIB=90+∠C/2
Circumcentre:
The point of intersection of the perpendicular bisectors of the three sides of a triangle is called its circumcentre.
The distance between the circumcentre and the three vertices of a triangle is always equal.
OA=OB =OC=R(circumradius)=abc/4A
∠BOC=2∠A
∠AOC=2∠B
∠AOB=2∠C
Location of circumcentre in various types of triangle:
Acute angle triangle: Lies inside the triangle
Obtuse angle triangle: Lies outside the triangle
Right angle triangle: Lies at the midpoint of the hypotenuse.
Orthocentre:
It is the point of intersection of all the three altitudes of the triangle.
∠BHC=180-∠A
∠AHB=180-∠C
∠AHC=180-∠B
Position of orthocentre inside the triangle:
Acute angled triangle: lies inside the triangle.
Obtuse angle triangle: lies outside the triangle on the backside of the obtuse angle. Orthocentre and circumcentre lie opposite to each other in obtuse angle triangle.
Right angle triangle: lies on the right angle of the triangle.
Centriod:
- It is the point of the intersection of the three median of the triangle. It is denoted by G.
- A centroid divides the area of the triangle in exactly three parts.
Medians:
- A line segment joining the midpoint of the side with the opposite vertex is called median.
- Median bisects the opposite side as well as divide the area of the triangle in two equal parts.
Some important tricks are as follows:
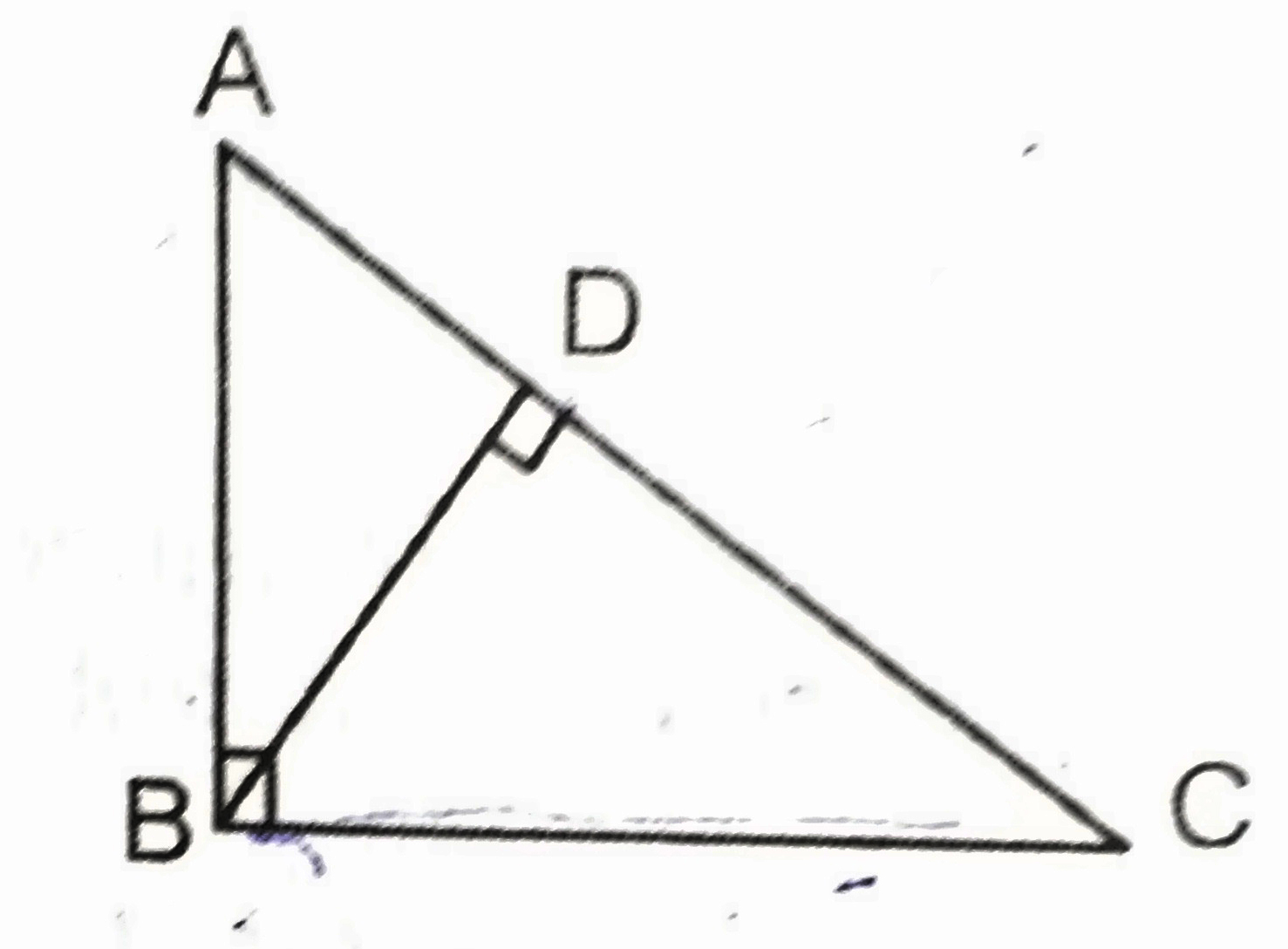
(1)In a right angle triangle ABC,∠B=90° & AC is the hypotenuse of the triangle. The perpendicular BD is dropped on the hypotenuse AC from the right angle vertex B,
BD=AB*BC/AC
AD=AB2/AC
CD=BC2/AC
1/BD=1/AB2 +1/BC2
(2)The ratio of the areas of the triangles with equal bases is equal to the ratio of their heights.
(3)The ratio of the areas of two triangles is equal to the ratio of products of base and its corresponding sides.
Area (Triangle ABC)/Area (Triangle PQR) =AC*BD/PR*QS
(4)If two triangles have the same base and lie between the same parallel lines then the area of the two triangles will be equal.
Area of Triangle ABC= Area of Triangle ADB
(5)In a triangle ABC, AE, CD and BF are the medians then
3(AB2+BC2+AC2) = 4(CD2+BF2+AE2)
6)Sum of any two sides of the triangle is always greater than the third sides.
(7)The difference of any two sides of a triangle is always less than the third sides.