Geometry Tricks – 1 [Important Formulae]

Many students asked me to share some geometry tricks. So here is the Part-1 :

(1) Be it algebra or geometry, such questions are always there that don’t deserve your rough space.

Like the above questions asks you the value of x. Now value of x can’t be negative in this context. Because CO = x – 3 and any negative value of ‘x’ will make CO negative, like if x = -8, then CO = -11. We know that side can never be negative. Hence all the options that have negative value for x are wrong.
Answer : (B)

In the above question a certain area is asked. Now see the options and observe that in options A, C and D if we take r=7, 2 and 1 respectively, then the area will become zero, and area can never be zero in this case, although value of ‘r’ can be 7, 2 or 1.
Answer : (B)
Note : Such questions are rare in geometry and in most of the questions you will have to pick up your pen, but still I shared these questions just to unleash the jugaad within you. Moreover, if you are able to solve even a single question with such approach, you will save at least 1 crucial minute in the examination hall.

(2) In geometry too, my beloved concept of ‘symmetry’ plays an important role. If in any question you find that some symmetrical expressions/equations are given, you can assume the triangle to be equilateral.

1. 1

In the above question you can assume that the triangle is equilateral. Then angles A, B and C will be 60. Hence sin²A + sin²B + sin²C = (√3/2)² + (√3/2)² + (√3/2)² = 9/4
Answer : (B)
Note : If in any question, the sides of a triangle are given (like a, b and c), then you can assume a = b = c, but make sure any additional detail is not given. Like in the above question that I solved, some additional equations were given, but then too I supposed the triangle to be equilateral only because the equation was symmetrical. Had the equation been unsymmetrical, I could not have been able to assume a =b =c

1. 2

Here the lengths of perpendiculars are given to be a, b and c. Note that no additional information is given, hence it is safe to assume a = b = c. Let the side of the triangle be ‘s’. The figure will look like this –

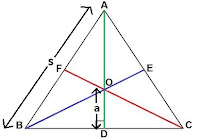
We have to establish a relation between ‘a’ and ‘s’. In an equilateral triangle, the incentre, orthocentre, circumcentre and centroid, all coincide. So you can calculate ‘a’, by which ever method you like.

a = inradius = s/2√3 [The inradius of an equilateral triangle is s/2√3 and the circumradius is s/√3]

Hence s = 2√3a

We know the formula for calculating the area of an equilateral triangle = (√3/4)s²

= (√3/4) (2√3a)²

= 3√3a²
Now put a = b = c in all the options and check which one will give 3√3a²
A) √3a

1. B) 3√2a²

C) √2a

1. D) 3√3a²

Answer : (D)

Moving on…

I have found that SSC has some real love with ‘Area of a triangle’ and it keeps on asking it again and again under different contexts. Like in Tier 2 (2014) around 5 questions asked area of triangles.
Therefore it is very important that you memorize all the possible formulas to calculate it. This will save you a lot of time.
Note : All the below questions are taken from a single paper [Tier-2, 2014].

Formula 1 : (Applicable only for Right-Angled Triangle)

1. 3

In the above question you may struggle to calculate the area. You can try this question yourself (with a timer), to see how much time you are taking…

There is a direct formula for such questions –

Apply this formula, area = (100^2 * sin30)/4 = 1250
Answer : (D)
Note : You can choose any of the angles of the triangle (except the 90 degree one) and you will get the same result. Like in the above question, the 3 angles of the triangle are 15, 75 and 90.
sin2*15 = sin30
sin2*75 = sin150
And we know that sin150 = sin30
Hence it doesn’t matter which angle you take. But to avoid any confusion, always take the smaller angle (15 in this case).

Next question –

1. 4

Again apply the same formula
Answer : (C)

Formula 2 :    ½*b*c*sinϴ

This formula is only applicable when ϴ lies between the sides ‘b’ and ‘c’.

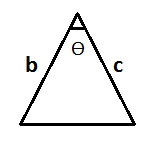
1. 5

Apply the formula, area = 1/2 * 10 * 10 * sin45
Answer : (D)

Formula 3 : Area of a triangle = r * S
where r = inradius
S = semi-perimeter

1. 6

Given, perimeter = 50, hence semi-perimeter = 25
Area = 6 * 25 = 150
Answer : (C)

Now when you know this formula, in Q. 2 above, where we had to establish relation between ‘s’ and ‘a’, you can establish it by applying this formula too.
Area of an equilateral triangle = (√3/4)s²
Area of a triangle = inradius * semi-perimeter = a * (3s)/2

Now,

a * (3s)/2 = (√3/4)s²

or s = 2√3a    [Same result]