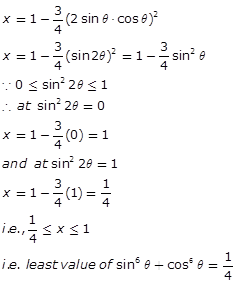Tricks to find Max and Min Value of Trigonometric identity

Dear Readers,

We are providing you trigonometric identity shortcuts which are usually asked in SSC Exams. Use these below short cuts to solve questions within minimum time. These shortcuts will be so  helpful for your upcoming SSC CGL Exam 2016.

Type-I

In case of sec²x, cosec²x, cot²x and tan²x, we cannot find the maximum value because they can have infinity as their maximum value. So in question containing these trigonometric identities, you will be asked to find the minimum values only. The typical question forms are listed below:

Example: -1

Find the Minimum value of 9 cos ²x + 2 sec ²x

sol – this equation is a typical example of our type-3 so apply the formula 2√ ab   so,

• Minimum Value = 2√ 9 x  2= 2√ 18

Example:-2

Find the Minimum value of 8 tan ²x + 7 cot ²x
sol – this equation is a typical example of our type-3 so apply the formula 2√ ab   so,

• Minimum Value = 2√ 8 x  7= 2√ 56

Type -II

Example -1

Find the Maximum and Minimum Value of 3 sin x + 4 cos y

Sol- If you find the question of this kind, apply the above formulae.

• Maximum Value = √ 9 + 16   = √ 25   = 5
• Minimum Value = – √ 9 + 16   = – √ 25   =  – 5

Example-2

Find the Maximum and Minimum Value of 3 sin x + 2 cos y

Sol- If you find the question of this kind, apply the above formulae.

• Maximum Value = √ 9 + 4   = √ 13
• Minimum Value = – √ 9 + 4   = – √ 13

   Type III

Example -1  

Find the maximum and Minimum Value of 3 sin ²x + 4 cos ²x

Sol- Here the 4> 3 so

•  Maximum Value = 4
• Minimum Value = 3

Example –2

Find the maximum and Minimum Value of 5 sin ²x + 3 cos ²x

Sol – Here 5>3

• Maximum Value = 5
• Minimum Value = 3

Type-IV

 Find the Minimum Value of  Sec ²x +  cosec ²x

Sol – 1 + tan ²x +  cosec ²x    ——————————————–(Sec ²x = 1 + tan ²x)

= 1+ tan ²x + 1 +  cot ²x ————————————————(cosec ²x = 1 + cot ²x )

=2 + tan ²x +  cot ²x—————————————————apply type-3 formula

=2 + 2 √ 1 x  1 = 2 + 2 =4

This topic creates a lot of problem for students during exam time.

Limit of the values of Trigonometric Functions :

(1)

(2)

(3)

(4)

(5)

(6)

QUESTIONS

(1)The greatest value of  is

(a)1

(b)1/2

(c) 0

(d) 

Ans.(a)

(2)What is the minimum value of

(a)  0

(b)3/4

(c)   2

(d) 1/4

Ans.  (b)

(3)Find the maximum value of 

(a) 

(b)  1

(c) 

(d)

Ans.  (d)      The maximum value of 

 The maximum value of 

(4)Find the minimum value of 

(a) 81

(b)41

(c)82

(d)90

Ans.   (a)

minimum value of

(5)  is maximum when is:

(a)15⁰

(b)30⁰

(c)45⁰

(d)  60⁰

Ans. (a)

The maximum value occurs when

(6)What is the maximum value of

(a)1/2

(b)1/4

(c)   1

(d)  None of these

Ans. (b)

(7)The greatest value of  is

(a)3⁵

(b)3⁴

(c)3

(d)3³

Ans.(a)

For maximum value

 maximum and maximum value is