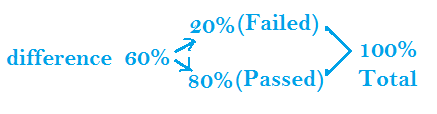Percentage Tricks & Tips
In Quantitative Aptitude Percentage concept helps to solving a problem of Data Interpretation, Profit and loss, SI and CI, Mixture and allegations etc.In this post i have covered introduction and the very common type of percentage problem that are frequently asked in various competitive exam.
Percentage is per‑cent which means parts per hundred(1/100).
If we have to convert percentage into fraction then it is divide by 100.
Example 1:‑ If we write 45% then its equal to 45/100 or in fraction 9/20or in decimal 0.45
If we have to convert fraction into percentage we have to multiple with 100.
Example 2:‑ if we write 3/5 in fraction it is equal to 60% =3/5×100=60.
Convert Percentage into Decimal:
- 20% = 20/100 = 0.5
Convert Decimal Into Percentage:
- 0.25 = (0.25 × 100) % = 25%
- 1.50 = (1.50 × 100) % = 150%
Majorly used values shown in Percent, Decimal and Fraction
This table will help you solve questions very fast and easily.Try to remember these fractions because it will save lot of time in your examination.

Types of Formulas and Short Tricks
Type 1: Percentage Increase/Decrease:
If the price of a commodity increases by R%, then the reduction in consumption so as not to increase the expenditure is: [R/ (100 + R)] x 100%
If the price of a commodity decreases by R%, then the increase in consumption so as not to decrease the expenditure is: [R/ (100 – R)] x 100%
Type 2: Results on Population:
Let the population of a town be P now and suppose it increases at the rate of R% per annum, then:
1.Population after n years = P(1 + R/100)n
2.Population n years ago =P/(1 + R/100)n
Type 3: Results on Depreciation:
Let the present value of a machine be P. Suppose it depreciates at the rate of R% per annum. Then:
1.Value of the machine after n years = P(1 – R/100)n
2.Value of the machine n years ago = P/[(1 – R/100)]n
3.If A is R% more than B, then B is less than A by= [R/ (100 + R)] x 100%
4.If A is R% less than B, then B is more than A by= [R/ (100 – R)] x 100%
Note: For two successive changes of x% and y%, net change = {x + y +xy/100}%
=> To express X% as a fraction
X%=X/100
For example: 56%
56%=56/100=14/25
=> Suppose A=120
B=150
(Q1)->A is a what percent(%) of B ?
Solution: X%(let) of B=A
(X/100) ×150 =120
∴ X=(120×100)/150
=80% ans
(Q2)->B is what % of A ?
solution: X% of A=B
(X/100) ×120 =150
∴ X=(150×100)/120
=125% ans.
(Q3)->B is how % more than A ?
Solution: difference=150-120=30
∴ Required percentage = (30×100)/120
=25% ans.
(Q4)->A is how % less than B ?
Solution: difference=150-120=30
∴ Required percentage = (30×100)/150
=20% ans.
PERCENTAGE PROBLEM CONCEPT:
* Suppose X increases by 40% means
X×(100+40)/100
=(X×140)/100
* Suppose X decreases by 30% means
X×(100-30)/100
=(X×70)/100
(Q1)->If salary of A is 300. now 40% increases then new salary of A.
Solution:

(Q2)->If salary of A is 300. now 40% decreases then new salary of A.
Solution:

(Q3)->Salary of A is 120.now what percent of salary increases then new salary of A is 144 ?
Solution:

% increase=(24×100)/120
= 20% Ans
Note: Rs 24, Rs 120 पर increase हो रहा है तो percentage हमेशा initial amount पर calculate किया जाता है न किincreased वाले amount पर .
(Q4)->If salary of A increases 40% then new salary of A is 490.find out initial salary
Solution:

Now
(X×140)/100=490
∴ X=(490×100)/140
=350Ans
COMMON TYPE OF PERCENTAGE PROBLEM THAT ARE FREQUENTLY ASKED IN VARIOUS COMPETITIVE EXAM.
(Q1)->If x% of Y% of 80 is the same as 25% of 900 then the value of xy is.
Solution: 80×(y/100)×(x/100)=900×(25/100)
4xy/500=25×9
∴xy=(25×9×500)/4
=28125 Ans
(Q2)->If 40% of 4/5 of 3/4 of a number is 48, then what is 1% of the same number?
Solution:Let the number be x
x×(3/4)×(4/5)×(40/100)=48
∴ x=(48×4×5×100)/(3×4×40)
=200
Now 1% of 200=200×(1/100)
=2 Ans.
(Q3)->What percent of 15 hours is 18 seconds?
Solution:x% of 15 hours = 18 seconds
x% of 15×60×60 seconds =18 seconds
15×60×60×(x/100)=18
∴ x=(18×100)/(15×60×60)
=1/30% Ans
(Q4)->What percent of 3.5 kg is 70 gms?
Solution:x% of 3.5 kg=70 gms
x%×3.5×1000 gms=70 gms
(x/100)×3.5×1000 gms=70gms
∴ x=(70×100)/3.5×1000
=2% Ans.
(Q5)->50% of a number when added to 50 is equal to the number.The number is.
Solution:Let the number be 100x
100x×(50/100)+50=100x
50x+50=100x
50x=50
∴ x=1
Number=100x
=100×1
=100 Ans
(Q6)->When 75 is added to 75% of a number,the answer is the number.Find 40% of that number.
Solution:Let the number be 100x
100x×75%+75=100x
=>100x ×(75/100)+75=100x
=>75x+75=100x
∴ x=3
Number=100x
=100×3
=300
Now 40% of 300=(300×40)/100
=120 Ans.
(Q7)->The number that is to be added to 10% of 320 to have the sum as 30% of 230 is.
Solution:Let the number to be added=x
320×(10/100)+x=(230×30)100
=>32+x=69
∴ x=37 Ans
(Q8)->If 60% of A=30% of B,B=40% of c,c=x% of A,then value of x is.
Solution:A×(60/100)=B×(30/100)
=>3A/5=3B/10
=>3A/5=(3/10)×(2C/5)
=>3A/5=6C/50
=>3A/5=(6/50)(Ax/100)
∴ x=(50×100×3A)/6A×5
=500 Ans
Rough:B=C×(40/100)
=2C/5
C =A×(x/100)
=Ax/100
(Q9)->51% of a whole number is 714. 25% of that number is.
Solution:Let the whole number be 100x
100x×51%=714
=>100x×(51/100)=714
∴ x=14
whole number=100x
=100×14
=1400 Ans.
Now, 25% of 1400=(25/100)×1400
=350 Ans.
(Q10)->83¹/3% of Rs 90 is equal to 60% of ?
Solution:90×83¹/3%=x×60%
90×(250 /3×100)=x×(60/100)
∴ x=(250×90×100)/(3×100×60)
=125 Ans.
(Q11)->If 8% of x=4% of y,then 20% of x is.
Option:(a)10% of y (b)16%of y (c)40% of y (c)80% of y
Solution:x×(8/100)=y×(4/100)
=>8x=4y
∴ x=y/2
let,
20% of x = z% of y
(20/100)×x=y×(z/100)
20x=yz
20×y/2 =yz [x=y/2]
∴ z=10% Ans
Option (a) Ans
(Q12)->If 30% of A is added to 40% of B,the answer is 80% of B.what percentage of A is B ?
Solution:A×(30/100)+B×(40/100)=B×(80/100)
=>(3A/10)+(4B/10)=8B/10
=>3A+4B=8B
=>3A=4B
∴ A/B=4/3
Now, x% of A=B
(x/100)×A=B
xA=B×100
x=100B/A
=100×3/4
=75% Ans.
IMPORTANT PERCENTAGE PROBLEM CONCEPTS SHORTCUT TRICKS FOR COMPETITIVE EXAM
(Q1)If Ravi salary is 25 % more than Raju’s salary the percentage by which Raju’s salary is less then Ravi salary.
Solution:BY TRICK
Required percentage=(25/100+25)×100)
=(25/125)×100
=20% Ans
(Q2)If A’s income is 50% less than that of B’s,then B’s income is what percent more than that of A ?
Solution: BY TRICK
Required percentage:(50/100−50)×100
=(50/50)×100
=100% Ans
(Q3)Two numbers are more than the third number by 20% and 50% respectively. The first number is what percent of the second number ?
Solution:Let third number=100
First number=120
Second number=150
∴ Required percentage=(120/150)×100
=80% Ans.
BY TRICK:
∴ Required percentage=(100+20/100+50)×100
=80% Ans.
(Q4)Two numbers are less than a third number by 30% and 37% respectively.The percent by which the second number is less than the first is.
Solution: Let the third number=100
First number=70
Second number=63
∴ Required percentage=(7/70)×100
=10% Ans.
(Q5)Two numbers are respectively 20% and 50% more than a third number. the ratio of the two numbers is.
Solution:Let the third number=100
First number=120
Second number=150
∴ Required ratio=120/150
=4/5
=4:5 Ans.
(Q6)25% of the annual salary of A is equal to 80% of the annual salary of the B.Monthly salary of B is 40% of the monthly salary of the C.Annual salary of C is Rs. 6 lac. what is the monthly salary of A?
Solution:monthly salary of C=600000/12
=Rs 50000
B’s monthly salary=(50000×40)/100
=Rs 20000
Annual salary of B=20000×12
=240000
Now,
Let Annual salary of A=X
( X×25)/100=(240000×80)/100
=>25X = 240000×80
∴ X=(240000×80)/25
=Rs 768000
monthly salary of A=768000/12
=Rs 64000 Ans.
(Q7)The monthly salaries of A and B together amount to Rs 40,000.A spends 85% of his salary and B, 95% of his salary.if now their saving is the same,then the salary(in Rs) of A is.
Solution:Let salary of A=X
salary of B=40000−X
Saving of A=15%
Saving of B=5%
Now according to question their saving are same so
( X×15)/100=(40000−X)×5/100
=>15X=200000−5X
=>20X=200000
∴ X=Rs 10000 Ans.
(Q8)Mohan donated 3% of his income to a charity and deposited 12% of the rest in the bank.if now he has Rs.12804,then his income was.
Solution:
Let income=100x

Now,
85.36x=12804
∴ x=150
income=100x
=100×150
=Rs 15000 Ans.
ROUGH:
(100X×3)/100=3X
rest=100x-3x=97x
deposit=12% of rest i.e 97x
(97x×12)/100
=11.64x
remaining=97x−11.64x=85.36x
(Q9)Mohan saves 14% of his salary while Shyam saves 22%. if both get the same salary and Shyam saves Rs. 1540, what is the saving of Mohan ?
Solution:According to question Shyam saves 22% i.e equal to 1540
now,
22%=1540
∴ 1%=1540/22
∴100%=(1540/22)×100
=Rs 7000 salaries of Shyam
saving of ram=(7000×14)/100
=Rs.980 Ans.
IMPORTANT PERCENTAGE SHORTCUT TRICKS,CONCEPTS AND PROBLEM FOR COMPETITIVE EXAM
FOR EXAMPLE
(Q1)Due to a decrease in price per kg. of sugar by 25% by how much percent, a housewife should increase quantity so that total expenditure remains same.
Solution:Let initial price=Rs. 100
Now,

% Increase=(25/75)×100
=33.33% Ans
Rough:New price=100×(100-25)/100
=Rs75
Concept:[जब Question में कहा जाए कि Total Expenditure same है तो आपलोगों को Quantity always price का reverse लेना है.
Explanation:[पहले housewife Rs 100 में 75 kg sugar खरीदती थी जब price decrease किया तो Rs 75में 100kg sugar खरीदती है तो इस तरह से housewife 25 kg अधिक sugar खरीद पा रही है ]
BY TRICK:
% increase=(25/100−25)×100
=(25/75)×100
=33.33% Ans.
(Q2)Due to increase in price per kg of sugar by 25% by how much percent, a housewife should decrease quantity so that total expenditure remains same.
Solution:Let initial price=Rs100
Now,

%decrease= (25/125)×100
=20% Ans
Rough:New price=100×(100+25)/100
=Rs125
BY TRICK:
%Decrease=(25/100+25)×100
=(25/125)×100
=20% Ans.
(Q3)If the price of sugar rises from Rs 6 per kg to Rs 7.50 per kg, a person to have no increase in his expenditure on sugar, will have to reduce his consumption of sugar by:
Solution:

% Reduce=(1.50/7.50)×100
=20% Ans
(Q4)The length of the rectangle is increased by 60%.By what percent would the breadth be decreased to maintain the same area?
Solution:Area of rectangle=Length×Breadth
Let initial length=100

% Decrease=(60/160)×100
=37½% Ans.
Concept:Breadth, Length का reverse लिया गया है because Area is same.
BY TRICK:
% Decrease=(60/100+60)×100
=(60/160)×100
=37½% Ans.
(Q5)One side of a square is increased by 30%.To maintain the same area,the other side will have to be decreased by.
Solution:Area of square=Side×Side
Let initial length of side=100
Now,

% Decrease=(30/130)×100
=23¹/3% Ans.
BY TRICK:
% Decrease=(30/100+30)×100
=23¹/3% Ans.
(Q6)The height of a triangle is increased by 10% to retain the original area of the triangle,its corresponding base must be decreased by:
Solution:Area of Triangle=½×base×height
Let initial height=100

%Decrease=(10/110)×100
=9¹/11% Ans.
BY TRICK:
%Decrease=(10/100+10)×100
=(10/110)×100
=9¹/11% Ans
I have discussed a common type percentage problem that is frequently asked in Bank PO SSC Railway exam.
For Example: The price of sugar having gone down by 10%,sharad can buy 6.2Kg more for Rs.279.The difference between the original and the reduced price(per Kg) is:
And another example is:The price of sugar is decreased by 25%.Therefore a family increases its consumption so that the decrement in the expenditure of sugar is only 15%.if the consumption of sugar is 30Kg before the decrement,what is the consumption now.
Common Type Of Percentage Problem That Is Frequently Asked In BANK PO SSC RAILWAY EXAM
(Q1)Due to increase in the price of sugar by 30% a man can buy 6kg less for Rs.520.then find out the original price per kg in Rs.?
Solution:Let original price=Rs 100
Now
Step-1

[Original price=Rs 100,New price=Rs130,Original quantity=130Kg,New Quantity=100Kg And Decreased quantity=30Kg]
Concept:According to Question A man can buy 6Kg less.But यहाँ पर 30Kg कम निकल रहा है,तो अब 30Kg को 6Kg बनाना होगा इसके लिए Quantity वाले part में 5 से Divide करना होगा|
[Concept in English:According to Question A man can buy 6Kg less.but here we got 30Kg less, so we will have to make 6kg, therefore, quantity divide by 5]
Step-2

price of 26 kg=Rs520
∴ Price of 1Kg=520/26
=Rs20 Ans.
Concept:[जब Expenditure same रहेगा तब इस process से solve करना है|इस Question में Expenditure same क्योंकि पहले Rs520 में जितना खरीदता था अब price increase होने से Rs520 में 6kg कम खरीद पा रहा है ]
BY TRICK:
Original price=(30×520)/(100+30)×6
=(30×520)/(130×6)
= Rs20 Ans.
(Q2)Due to a decrease in the price of sugar by 20% a man can buy 4Kg more for Rs80 then find the original price per Kg in Kg?
Solution:Let original price=Rs100
Step-1

[Original price=Rs 100,New price=Rs80,Original quantity=80Kg,New Quantity=100Kg And Increased quantity=20Kg]
Concept:According to Question A man can buy 4Kg more.But यहाँ पर 20Kg अधिक निकल रहा है,तो अब 20Kg को 4Kg बनाना होगा इसके लिए Quantity वाले part में 5 से Divide करना होगा|
[Concept in English:According to Question A man can buy 4Kg more.but here we got 20Kg more, so we will have to make 4kg, therefore, quantity divide by 5]
Step-2

the price of 16kg=Rs80
∴ price of 1Kg=80/16
=Rs 5 Ans.
BY TRICK:
Original price=(20×80)/(100-20)×4
=(20×80)/(80×4)
= Rs.5 Ans.
(Q3)A reduction of 21% in the price of wheat enables a person to buy 10.5kg more for Rs.100.what is the reduced price per Kg?
Solution:Let original price=Rs.100
Step-1

Step-2

Price of 50Kg=Rs.100
∴price of 1Kg=100/50
=Rs.2 Ans
BY TRICK:
Reduced price=(21×100)/(100×10.5)
=Rs.2 Ans
(Q4)The price of sugar having gone down by 10%,sharad can buy 6.2Kg more for Rs.279.The difference between the original and the reduced price(per Kg) is:
Solution:Let original price=Rs.100
Step-1:

Step-2:

(1)Original price:
Price of 90×0.62Kg=Rs.279
∴ price of 1Kg=279/(90×0.62)
=Rs.5/Kg Ans.
(2)Reduced price:
Price of 100×0.62Kg=Rs.279
∴ price of 1Kg=279/(100×0.62)
=Rs.4.5/Kg Ans
Difference=5-4.5
=Rs.0.5 Ans.
BY TRICK:
Original price=10×279/(100-10)×6.2
=10×279/(90×6.2)
=Rs.5/Kg
Reduced price=10×279/(100×6.2)
=Rs.4.5/Kg
IMPORTANT PERCENTAGE PROBLEM CONCEPTS AND SHORTCUT TRICKS FOR BANK PO SSC RAILWAY EXAM TYPE-4.1
(Q1)The price of sugar is increased by 30%.Therefore a family reduces its consumption so that the increment in the expenditure of sugar is only 10%.if the consumption of sugar is 26Kg before the increment,what is the consumption now.
Solution:We know that

∴ X=286/13
=22Kg Ans
ROUGH:
Rs10 increased by 30% then,
=10×(100+30)/100
=Rs13
Rs260 increased by 10% then,
260×(100+10)/100
=(260×110)/100
=Rs286
BY TRICK:
Consumption=26×(100+10)/(100+30)
=26×110/130
=22Kg Ans.
(Q2)The price of sugar is decreased by 25%.Therefore a family increases its consumption so that the decrement in the expenditure of sugar is only 15%.if the consumption of sugar is 30Kg before the decrement,what is the consumption now.
Solution:

∴ X=255/7.50
=34Kg Ans.
ROUGH:
Rs300 decreased by 15% then
300×(100-15)/100
=(300×85)/100
=255
Rs10 decreased by 25% then,
10×(100-25)/100
=(10×75)/100
=7.50
BY TRICK:
consumption:30×(100-15)/100-25
=(30×85)/75
=34Kg Ans.
Common Type Percentage Problem That Is Frequently Asked in BANK PO,SSC,Railways Exam
(Q1)Due to increase in the price of sugar by 20%.the consumption reduces by 30%.then find the percentage effect on total expenditure from it.
Solution:

%Effect=(16×100)/100
=16% Ans
CONCEPT:[यदि Price and Quantity/Consumption दोनों में change हो रहा हो तो Price and Quantity/Consumption को 100 मानना(let) है]
BY TRICK:
%Effect=(20-30-(20×30)/100)%
=-16%
=16% Decrease
Note:[-ve sign means decreases]
(Q2)The price of an article is reduced by 25% but the daily sale of the article is increased by 30%.the net effect on the daily sale receipts is.
Solution:

Net effect=(1×100)/40
=2½% Ans
BY TRICK:
Net effect=(-25+30-(25×30)/100)
=-2½% [-ve sign means decreases]
=2½% Ans
(Q3)If side of a square is increased by 10% then the percentage change in its area will be?
Solution:Area of square=side×side

%increase or change=(21×100)/100
=21% Ans
BY TRICK:
% change=(10+10+(10×10)/100)%
=(20+1)%
=21% Ans.
(Q4)If the radius of a circle is increased by 25% then area of circle will be increased by.
Solution:Area of circle=πr² [where r=radius]

% increase=(9×100)/16
=56.25% Ans.
BY TRICK:
%Increase=(25+25+(25×25)/100)%
=50+(25/4)%
=56.25% Ans.
(Q5)If radius is increased by 10% and height is decreased by 20% of cylinder. then find the percent change in volume of the cylinder.
Solution:Volume of cylinder=πr²h [where r=radius and h=height]

% change or increase=(32×100)/1000
=3.2% Ans
BY TRICK:
(10+10+(10×10)/100)%
now % change
=(21-20-(21×20)/100)%
=1-42/10
=-32/10
=-3.2%
i.e 3.2% decreases
(Q6)The percentage increases in the surface area of a cube when side is doubled .
Solution:Surface area of cube=6a²

% increase=(3×100)/1
=300% Ans
(Q7)The numerator of a fraction is increased by 20% and denominator is decreased by 20%.The value of the fraction becomes 4/5.The original fraction is.
Solution:Let original fraction =X/Y [where X=numerator and Y=denominator]

Now,
6X/4Y=4/5
=>30X=16Y
∴X/Y=16/30
=8/15 Ans.
(Q8)The price of an article was first increased by 10% and then again by 20%.If the last increased price be Rs 33,The original price was.
Solution:

% increase=(32×100)/100
=32% Ans.
Now,
Let original price=x

∴ x=(33×100)/132
=Rs 25 Ans.
BY TRICK:
% increase=(10+20+(10×20)100)%
= 32%
Now
Let original price=x

x×(100+32)/100=33
∴ x=(33×100)/132
=Rs 25 Ans.
(Q9)The cost of an article was Rs 75.The cost was first increased by 20% and later on it was reduced by 20%. The present cost of the article is.
Solution:

%Decrease=(1×100)/25
=4% Ans.
Now present cost of the article is:

Rough:
Rs 75 increased by 20%
i.e 75×(100+20)/100
=(75×120)/100
=Rs 90
Rs 75 Reduced by 20%
i.e 75×(100-20)/100
=(75×80)/100
=Rs 60
BY TRICK:
(20-20-(20×20)/100)%
=-4%=4% decrease
Now present cost of the article is:

(Q10)The difference between the value of the number increased by 20% and the value of the number decreased by 25% is 36. Find the number.
Solution:Let number =100x

now,
120x-75x=36
∴ 45x=36
∴ x=36/45
Number=100x=100×(36/45)
=80 Ans.
(Q11)A number is first decreased by 20%.The decreased number is then increased by 20%.The resulting number is less than the original number by 20.then the original number is.
Solution:

now,
100x-96x=20
4x=20
∴ x=5
original number=100x
=100×5
=500 Ans.
FOR EXAMPLE:
(Q1) A candidate who scores 30% fails by 5 marks, while another candidate who scores 40% marks get 10 more then minimum pass marks. The minimum marks required to pass are.
Solution:Let total marks=100x
Now,
100x×(30/100)+5=100x×(40/100)-10
=>30x+5=40x-10
=>30x-40x=-10-5
=.-10x=-15
∴x=15/10
Total marks=100x
=100×(15/10)
=150
∴ minimum marks=100x×(30/100)+5
=100×(15/10)×(30/100)+5
=50 Ans
Concepts:[According to question A candidate who scores 30% fails by 5 marks.that means इस candidate को minimum pass marks के लिए 5 marks अधिक लना चाहिए था i.e 100x×(30/100)+5 marks लाना चाहिए था|
now another candidate who scores 40% marks get 10 more than minimum passing marks.that means इस candidate को minimum pass marks के लिए 10 marks कम लाना चाहिए था i.e 100x×(40/100)-10 लाना चाहिए था|]
(Q2)In an examination, a candidate must secure 40% marks to pass. A candidate, who gets 220 marks fails by 20 marks. what are the maximum marks for the examination?
Solution:Let maximum marks=100x
now,
100x×(40/100) =220+20
40x=240
∴ x=6
maximum marks=100x
=100×6
600 Ans.
Concept:[220 marks लाया and 20 marks से fail हो गया that means उसे pass होने के लिये (220+20)marks लाना होगा]
(Q3)In an examination, there are three papers and a candidate has got 35% of the total to pass. in one paper ,he gets 62 out of 150 and in the second 35 out of 150. how much he get, out of 180, In the third paper to just qualify for a pass.
Solution:Let the marks required in the third paper= x.
then,
(62+35+x)=35% of(150+150+180)
=>97+x=(35/100)×480
∴ x=168-97
=71 Ans.
(Q4)In an examination, there are three subjects of 100 marks each. A student scores 60% in the first subject and 80% in the second subject. He scored 70% in aggregate. His percentage of marks in the third subjects is.
Solution:let percentage marks in third subjects=x
then,
60+80+x=70% of (100+100+100)
=>140x=(70/100)×300
∴ x=70 i.e 70% Ans.
(Q5)In an examination,65% of the students passed in mathematics, 48% passed in physics and 30% passed in both. How much percent of students failed in both the subjects ?
Solution:

Students passed only in mathematics=65%-30%=35%
Students passed only in physics=48%-30%=18%
students passed in both subjects=30%
total pass=35%+18%+30%
=83%
∴ total failed in both subjects=100%-83%
=17% Ans.
BY TRICK:
percentage of students who passed in either mathematics or physics or both=(65+48-30)%=83%
∴ total failed in both subjects=100%-83%
=17% Ans.
(Q6)In an examination, 75% candidate who passed in English and 60% passed in mathematics. 25% failed in both the subjects. If 240 candidate passed in both.Find the total number of candidates.
Solution:Let x candidates passed in both subjects.
percentage of students who passed in either English or mathematics or both=(75+60-x)%
=>75%=(135-x)%
∴ x=60%
Now,
60%=240
∴ 1%=240/60
∴ 100%=(240/60)×100
=400 candidate Ans.
Concept:[25% failed in both subjects it means only 75% candidates passed in either English or mathematics or both]
(Q7)In an examination A got 25% marks more than B, B got 10% less than C and C got 25% more than D. if D got 320 marks out of 500, the marks obtained by A.
Solution:

(Q8)Three sets of 40,50 and 60 students appeared for an examination and the pass percentage was 100,90 and 80 respectively. The pass percentage of the whole set is.
Solution:pass percentage of the whole set=(40×100+90×50+60×80)/(40+50+60)
=88²/3% Ans.
(Q1)In an election, there were only two candidates. one of the candidates secured 40% of votes and is defeated by the other candidate by 298 votes. The total number of votes polled is.
Solution:Let total votes=100x

Now,
60x-40x=298
=>20x=298
∴ x=298/20
=14.6
Total votes=100x
=100×14.6
=1460 votes Ans.
Rough:
100x×(40/100)
=40x
100x×(60/100)
=60x
(Q2)In an election between two candidates, the candidate getting 60% of the votes polled,is elected by a majority of 14000 votes . The number of votes polled by the winning candidate is.
Solution:

60x-40x=14000
20x=14000
∴ x=14000/20
=700
Number of votes polled by the winning candidate=60x
=60×700
=42000 votes Ans.
(Q3)8% of the votes in an election did not cast their votes. In this election,there only two candidates.The winner by obtaining 48% of the total votes defeated his contestant by 1100 votes. The total number of voters in the election was.
Solution:

Now,
48x-44x=1100
=>4x=1100
∴ x=1100/4
Total number of voter=100x
=100×(1100/4)
=27500 voters Ans
Concept:[8% of the voters in an election did not cast their votes, it means only 92% voter cast their votes now winner candidates secure 48% votes ∴ Loser candidate=92%-48%=44%]
(Q4)In an election between two candidates,One got 55% of the total valid votes,20% of the votes were invalid.If the total number of votes was 7500,the number of valid votes that the other candidate got,was.
Solution:Total number of votes =7500
20% invalid votes
i.e 7500×(20/100)
=1500 invalid votes.
now valid votes=7500-1500=6000 votes
one candidate got 55% of the total valid votes
i.e 6000×(55/100)
=3300 votes
2nd candidate got=6000-3300
=2700 votes Ans.
(Q5)10% of the voters did not cast their vote in an election between two candidates.10% of the votes polled were found invalid. The successful candidate got 54% of the valid votes and won by a majority of 1620 votes. The numbers of voters enrolled on the voter list.
Solution:Let the numbers of voters enrolled on the voter list=100x

Now,
81x×(54/100)-81x×(46/100)=1620
81x[(54/100)-(46/100)]=1620
∴ x=(1620×100)/(81×8)
=250
The numbers of voters enrolled on the voter list=100x
=100×250
=25000 Ans.
Rough:
10% did not cast their votes
i.e 100x×(10/100)
=10x voter did not cast vote
∴ casting vote=100x-10x=90x
10% invalid votes of 90x
i.e 90x(10/100)
=9x
∴ valid votes=90x-9x=81x
(Q1)Mohan gives 35% of the money he had to his wife and gave 50% of the money he had to his sons. The remaining amount of 11,250 he kept for himself. what was the total amount of money Mohan had?
Solution:Let total amount of money Mohan had=100x

Now,
15x=11250
∴ x=11250/15
=750
Total amount of money Mohan had=100x
=100×750
=75000 Ans.
Rough:
Total money gives by Mohan to his wife+son=35%+50%=85%
Now,
100x×(85/100)
=85%
remaining=100x-85x=15x
(Q2)Mr. Nand spent 20% of his monthly income on food and 15% on children’s education, 40% of the remaining he spent on entertainment and transport together and 30% on medical.He is left with an amount of 8775 after all these expenditures. What is Mr. Nand monthly income?
Solution:Let monthly income of Mr. Nand=100x

19.5x=8775
∴ x=8775/19.5
= 450
monthly income of Mr. Nand=100x
=100×450
=45000 Ans.
Rough:
Total spent on Food+Education=20%+15%=35%
i.e 100x(35/100)
=35x
Remaining=100x-35x=65x
Total spent on entertainment+Transport+Medical=70%
i.e 65x(70/100)
=45.5x
Remaining=65x-45.5x=19.5x
(Q3)Mohan had a certain amount with him. He spent 20% of that to buy an article and 5% of the Remaining on Transport, then he gifted Rs 120. If he is left with Rs 1400, the amount he spent on transport is.
Solution:Let certain amount=100x

76x-120=1400
=>76x=1520
∴ x=1520/76
=20
Transport=4x
=4×20
=Rs 80 Ans.
(Q4)Aman spends 40% of the amount he received from his father on Hostel expenses, 20% on Books and Stationary and 50% of the remaining on Transport. He saves Rs 450 which is half the Remaining amount after spending on Hostel expenses,Books etc. and Transport. How much money did he get from his father?
Solution:Let Aman get money from his father=100x

10x=450
∴ x=45
Aman get money from his father=100x
=100×45
=Rs 4500 Ans.
Rough:
Total spent on Hostel+(Books+Stationary)=40%+20%=60%
i.e 100x×(60/100)
=60x
Remaining=100x-60x=40x
50% remaining on transport
i.e 40x×(50/100)
=20x
Remaining=40x-20x=20x
(Q5)A man spends 75% of his income. His income is increased by 20% and he increased his expenditure by 10%. His saving is increased by.
Solution:Let income=100x

Expenditure(i.e spend) is increased by 10% than new Expenditure
=75x×(100+10)/100
=75x×(110/100)
=82.5x
New saving=120x-82.5x=37.5x
Increased saving=37.5x-25x=12.50x
% increase=(12.50x×100)/25x
=50% Ans
(Q6)The monthly salaries of A and B together amount to Rs 40000. A spends 85% of his salary and B, 95% of his salary. If now their saving is the same, then the salary of A.
Solution:Let salary of A=100x
Salary of B=40000-100x
A spends 85% of his salary that means A saved 15% salary
∴ Saving of A=100x(15/100)
=15x
B spends 95% of his salary that means B saved 5% salary
∴ Saving of B=(40000-100x)×(5/100)
=(40000-100x)/20
According to question their saving are same so,
15x=(40000-100x)/20
300x=40000-100x
∴ x=40000/400
= 100
Now,
Salary of A=100x
=100×100
=Rs 10000 Ans.
(Q1)The population of a town increases by 5% every year. If the present population is 9261, The population 3 Years ago was.
Solution:F.Q=I.Q×M.F
Where, I.Q=Initial Quantity
F.Q=Final Quantity
M.F=Multiplying Factor
Now
F.Q=I.Q×M.F
9261=I.Q×(105/100)×(105/100)×(105/100)
I.Q=(9261×100×100×100)/(105×105×105)
=8000 Ans
CONCEPT:[इस Type के Question को Solve करते Time आपलोगो को सिर्फ इन बातों पर ध्यान रखना है Question में After n Years का value निकालने के लिए कह रहा है या n Years Ago का | (1)यदि Question में After n Years का value निकालने के लिए कह रहा हो तो Present value जो Question में दिया होगा वह Initial Quantity होगा| (2) यदि Question में n Years Ago का value निकालने के लिए कह रहा हो तो Present value जो Question में दिया होगा वह Final Quantity होगा|]
(Q2)The present population of a city is 180000. If it increases at the rate of 10%per annum,its population after 2 years will be.
Solution:F.Q=I.Q×M.F
F.Q=180000×(110/100)×(110/100)
=217800 Ans.
(Q3)The present price of a scooter is 7290. If its value decreases every year by 10%, then its value after 3 years back was.
Solution:F.Q=I.Q×M.F
7290=I.Q×(90/100)×(90/100)×(90/100)
∴ I.Q=(7290×100×100×100)/(90×90×90)
=10000 Ans.
(Q4)In a factory, the production of cycles rose to 48,400 from 40,000 in 2 years. The rate of growth per annum is.
Solution:Let rate of growth=x%
F.Q=I.Q×M.F
48,400=40000×((100+x)/100)×(100+x)/100
48,400/4=(100+x)²
12100=(100+x)²
(110)²=(100+x)²
100+x=110
∴ x=10% Ans
(Q5)The population of a village was 9800. In a year with the increase in the population of males by 8% and that of females by 5%, the population of the village become 10458.What was the number of males in the village before increase?
Solution:Let the number of males=x
∴ number of females=9800-x
x×(108/100)+(9800-x)×(105/100)=10458
=>108x+9800×105-105x=1045800
=>3x=1045800-1029000
=16800
∴ x=16800/3
=5600 Ans.
Percentage Shortcut Tricks Bank PO SSC Railway Exams type-9.1.
(Q1)A large watermelon weighs 20kg with 96% of its weight being water. It is allowed to stand in the sun and some of the water evaporates so that only 95% of its weight is water.Its reduced weight will be:
Solution:

Weight of fresh watermelon=20Kg
the weight of fresh pulp=20×(4/100)
=0.8Kg
Now,
Concept:[watermelon में से water सूखेगा न कि pulp. pulp तो always same ही रहेगा चाहे Fresh हो या Dry ]
so,
5%=0.8Kg
1%=0.8/5 Kg
∴ 100%=(0.8/5)×100 Kg
=16 Kg Ans.
(Q2)Fresh grapes contain 80% water while Dry grapes contain 10% water. If the weight of dry grapes is 500Kg then what is its total weight when it is fresh.
Solution:

Weight of Dry grapes=500Kg
the weight of Dry pulp=500×(90/100)
=450Kg
Now,
Concept:[Grapes में से water सूखेगा न कि pulp. pulp तो always same ही रहेगा चाहे Fresh हो या Dry ]
so,
20%=450Kg
1%=450/20 Kg
∴ 100%=(450/20)×100 Kg
=2250 Kg Ans.
Tricks to solve Percentage Problems
Percentage is a fraction whose denominator is always 100. x percentage is represented by x%.
To express x% as a fraction :
x% = x/100
= 1/10 (means 1 part out of 10 parts)
To express x/y as a percentage :
We know that x/y = (x/y× 100 )
and 0.8 = ( 8/10 ×100 )% = 80%
If the price of a commodity increases by R%, then reduction in consumption as not to increase the expenditure is-
[ R/(100+R)×100 ] %
If the price of a commodity decreases by R%, then the increase in consumption as not to decrease the expenditure is –
[ R/(100-R)×100 ] %
Result on Population :
Let the population of a town be P now and suppose increases the rate of R% per annum, then :
- Population after n years = P ( 1+ R/100 )n
- Population n years ago = P /( 1+ R/100 )n
Result on Depreciation :
Let the present value of a machine be P. Suppose depreciates at the rate of R% per annum Then :
1. Value of the machine after n Years
- If A is R% more than B, then B is less than A by
[ R/(100+R)×100 ]%
- Net % change = x + y + xy/100
Some Observation
#1
If 20% candidate failed in an exam then observations are
- 80% represent passed in exam
- 100% represent total appeared in exam
- (80%-20%) = 60% represent difference between passed and failed candidate in exam
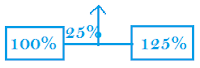
#2
- 100% represent the old number
- 125% represent the new number.
#3
Remember it :
Examples
#1
#2
- 75% of Ram’s income ?
- 1/4 part of Ram’s income ?
- 1/3 part of Ram’s income ?
Sol :
Trick : 1200 / 40 × 75 = Rs. 2250/-
Trick :
Practice Problems on Percentage
- Veena bought a watch costing Rs. 1404 including sales tax at 8%. She asked the shopkeeper to reduce the price of the watch so that she can save the amount equal to the tax. The reduction of the price of the watch is?
A. Rs.108
B. Rs.104
C. Rs.112
D. Rs.120
E. None of these - A Sales Executive gets a commission on total sales at 8%. If the sale is exceeded Rs.10,000 he gets an additional commission as a bonus of 4% on the excess of sales over Rs.10,000. If he gets the total commission of Rs.950, then the bonus he received is?
A. 40
B. 50
C. 36
D. 48
E. None of these - In a College there are 1800 students. Last day except 4% of the boys all the students were present in the college. Today except 5% of the girls all the students are present in the college, but in both the days number of students present in the college, were same. The number of girls in the college is?
A. 1000
B. 400
C. 800
D. 600
E. 1200 - In a library 60% of the books are in Hindi, 60% of the remaining books are in English rest of the books are in Malayalam. If there are 4800 books in English, then the total number of books in Malayalam are?
A. 3400
B. 3500
C. 3100
D. 3200
E.None of these - 80% of a small number is 4 less than 40% of a larger number. The larger number is 125 greater than the smaller one. The sum of these two numbers is
A. 325
B. 345
C. 355
D. 365
E. None of these - In a private company 60% of the employees are men and 48% of the employees are Engineer and 66.6% of Engineers are men. The percentage of women who are not engineers is?
A. 60%
B. 50%
C. 55%
D. 65%
E. 45% - Initially, Suresh has Rs.200 in his paytm wallet then he increased it by 20%. Once again he increased his amount by 25%. The final value of money in his wallet will be how much % greater than the initial amount?
A. 40%
B. 50%
C. 80%
D. 60%
E. None of these - Mr.Ramesh gives 10% of some amount to his wife and 10% of the remaining to hospital expenses and again 10% of the remaining amount to charity. Then he has only Rs.7290 with him. What is the initial sum of money with that person?
A. Rs.8000
B. Rs.9000
C. Rs.10000
D. Rs.20000
E. Rs.17200 - Initially, a shopkeeper had “x” pens. A customer bought 10% of pens from “x” then another customer bought 20% of the remaining pens after that one more customer purchased 25% of the remaining pens. Finally, shopkeeper is left with 270 pens in his shop. How many pens were there initially in his shop?
A. 200
B. 800
C. 400
D. 600
E. 500 - The cost of packaging of the oranges is 20% the cost of fresh oranges themselves. The cost of oranges increased by 30% but the cost of packaging decreased by 50%, then the percentage change of the cost of packed oranges, if the cost of packed oranges is equal to the sum of the cost of fresh oranges and cost of packaging
A. 14.5%
B. 16.66%
C. 14.33%
D. 13.66%
E. None of these
- Cost Price of two laptops is same. One of the laptops is sold at a profit of 15% and the Selling Price of another one laptop is Rs. 3400 more than the first one. The net profit is 20%. What is the Cost Price of Each laptop?
A.36000
B.40000
C.48000
D.34000
E.None of these - In an office there are 40% female employees. 50% of the male employees are UG graduates. The total 52% of employees are UG graduates out of 1800 employees. What is the number of female employees who are UG graduates?
A. 362
B. 412
C. 396
D. 428
E. None of these - Ravi got 70% in English and 56% in Biology and the maximum marks of both papers is 100. What percent does he score in Maths, if he scores 60% marks in all the three subjects?. Maximum Marks of Maths paper is 200.
A. 30%
B. 40%
C. 45%
D. 25%
E. 57% - Ankita is 25 years old. If Rahul’s age is 25% greater than that of Ankita then how much percent Ankita’s age is less than Rahul’s age?
A. 40%
B. 35%
C. 10%
D. 20%
E.None of these - Mr.Ravi’s salary was reduced by 25% for three months. But after the three months, his salary was increased to the original salary. What is the percentage increase in salary of Mr.Ravi?
A. 33.33%
B. 42.85%
C. 28.56%
D. 16.66%
E. None of these - In an election only two candidates A and B contested 30% of the voters did not vote and 1600 votes were declared as invalid. The winner, A got 4800 votes more than his opponent thus he secured 51% votes of the total voters on the voter list. Percentage votes of the loser candidate, B out of the total voters on the voter list is:
A. 5.6%
B. 3%
C. 6.2%
D. 5%
E. 4.6% - In a school there are 2000 students. On January 2nd, all the students were present in the school except 4% of the boys and on January 3rd, all the students are present in the school except 28/3% of the girls, but in both the days number of students present in the school, were same. The number of girls in the school is?
A. 400
B. 1200
C. 800
D. 600
E. None of these - A school has raised 75% of the amount it needs for a new building by receiving an average donation of Rs. 1200 from the parents of the students. The people already solicited represents the parents of 60% of the students. If the School is to raise exactly the amount needed for the new building, what should be the average donation from the remaining students to be solicited?
A. Rs.800
B. Rs.900
C. Rs.850
D. Rs.600
E. Rs.720 - The monthly income of Shyama and Kamal together is Rs.28000. The income of Shyama and Kamal is increased by 25% and 12.5% respectively. The new income of Kamal becomes 120% of the new salary of Shyama. What is the new income of Shyama?
A. Rs.12000
B. Rs.18000
C. Rs.14000
D. Rs.16000
E. Rs.15000 - 500 kg of ore contained a certain amount of iron. After the first blast furnace process, 200 kg of slag containing 12.5% of iron was removed. The percentage of iron in the remaining ore was found to be 20% more than the percentage in the original ore. How many kg of iron were there in the original 500 kg ore?
A. 54.2
B. 58.5
C. 46.3
D. 42.4
E. 89.2
- In a class of 60 students , 40% of the students passed in Reasoning, 5% of the students failed in Quants and Reasoning, and 20% of the students passed in both the subjects. Find the number of student passed only in Quants?
1.17
2.33
3.23
4.37
5.None of these - The maximum marks per paper in 3 subjects in Mathematics , Physics and Chemistry are set in the ratio 1 : 2 : 3 respectively. Giri obtained 40% in Mathematics, 60% in Physics and 35% in Chemistry papers. What is overall percentage marks did he get overall?
1.44%
2.32%
3.50%
4.60%
5.None of these - In an examination, 50% of the students passed in Science and 75% passed in Social, while 20% students failed in both the subjects. If 270 students passed in both subjects, find the total number of students who appeared in the exam?
1.400
2.540
3.600
4.750
5.None of these - Fresh fruits contain 75% while dry fruits contain 20% water. If the weight of dry fruits is 300 kg, what was its total weight when it was fresh?
1.900kg
2.850kg
3.920kg
4.960kg
5.None of these - In a college election 35% voted for Person A, whereas 42% voted for Person B. The remaining people were not vote to any person. If the difference between those who vote for Person B in the election and those who are uncertain was 570, how many people are participated in the college election?
1.1500
2.2000
3.2100
4.1700
5.None of these - In a factory there are three types of bulbs L1, L2 and L3 which produces 20%, 15% and 32% of the total products respectively. L1, L2 and L3 produces 3%, 7% and 2% defective products, respectively. Find the percentage of non-defective products ?
1.46%
2.30%
3.53%
4.64%
5.None of these - In a class of 500 students ,65% are boys. 20% of the girls and 40% of the boys failed the exam.Find the of students in the school passed the exam?
1.335
2.270
3.400
4.362
5.None of these - The population of village increases at the rate of 6% per annum. There is an additional increase of 2% in the population due to rural development .Therefore the percentage increase in the population after 2 years will be
1.15.46%
2.16.64%
3.14.46%
4.12.56%
5.None of these - The total salary of Guagn and Harish in an organization is Rs 30000. If the salary of Gugan increase by 5% and salary of Harish increase by 7%, then their total salary would increase to Rs 31800. Find the salary of Harish ?
1.Rs.10,000
2.Rs.15,000
3.Rs.18,000
4.Rs.12,000
5.None of these - In an examination 70% candidates passed in prelims and 55% candidates passed in Mains. If 62% candidates passed in both these subjects, then what per cent of candidates failed in both the exams?
1.37%
2.26%
3.43%
4.15%
5.None of these
- In a class, 60% of the students are boys and in an examination, 80% of the girls scored more than 40 marks(Maximum Marks:150). If 60% of the total students scored more than 40 marks in the same exam, what is the fraction of the boys who scored 40 marks or less.
A.8/15
B.7/15
C.4/5
D.1/5 - In an election 10% of the voters on the voters’ list did not cast votes and 60 voters cast their ballot papers blank. There were only two candidates. The winner was supported by 47% of all voters in the list and he got 308 votes more than his rival. The number of voters on the list was:
A. 3600
B. 6200
C. 4575
D. 6028 - Deepak was to get a 50% hike in his pay but the computer operator wrongly typed the figure as 80% and printed the new pay slip. He received this revised salary for three months before the organization realized the mistake. What percentage of his correct new salary will get in the fourth month, if the excess paid to him in the previous three months is to be deducted from his fourth month?
A. 30%
B. 40%
C. 45%
D. 25% - The prices of two articles are in the ratio 3 : 4. If the price of the first article be increased by 10% and that of the second by Rs. 4, the original ratio remains the same. The original price of the second article is
A. Rs.40
B. Rs.35
C. Rs.10
D. Rs.30 - The ratio of the number of boys and girls in a school is 3:2. If 20% of the boys and 25% of the girls are scholarship holders, the percentage of the students who are not scholarship holders is
A. 30%
B. 60%
C. 75%
D. 78% - Sohan spends 23% of an amount of money on an insurance policy, 33% on food, 19% on children’s education and 16% on recreation. He deposits the remaining amount of Rs. 504 in bank. How much total amount did he spend on food and insurance policy together?
A. Rs.3146
B. Rs.3126
C. Rs.3136
D. Rs.3048 - Deepika went to a fruit shop with a certain amount of money. She retains 15% of her money for auto fare. She can buy either 40 apples or 70 oranges with that remaining amount. If she buys 35 oranges, how many more apples she can buy?
A. 35
B. 40
C. 15
D. 20 - The price of a car is Rs. 4,50,000. It was insured to 80% of its price. The car was damaged completely in an accident and the insurance company paid 90% of the insurance. What was the difference between the price of the car and the amount received?
A. Rs.1,76,375
B. Rs.3,24,000
C. Rs.1,82,150
D. Rs.1,26,000 - The tank-full petrol in Arun’s motor-cycle last for 10 days. If he starts using 25% more every day, how many days will the tank-full petrol last?
A.4
B.6
C.8
D.10 - Last year there were 610 boys in a school. The number decreased by 20 percent this year. How many girls are there in the school if the number of girls is 175 percent of the total number of boys in the school this year ?
A. 854
B. 848
C. 798
D. 782