Ratio & Proportion Tricks & Tips
Ratio & Proportion Short-Cut Tricks & Tips : Ratio & Proportion Short-Cut Tricks & Tips Question Pdf for Banking, SSC, RRB, FCI, Railway, UPSC, State PCS, Insurance & other Competitive exams. Ratio & Proportion Short-Cut Tricks & Tips shortcut Tricks Pdf, Ratio & Proportion Short-Cut Tricks & Tips MCQ, Ratio & Proportion Short-Cut Tricks & Tips Objective Question & Answer Pdf. “Ratio & Proportion Short-Cut Tricks & Tips Questions PDF” In this post we are providing you the Ratio & Proportion Short-Cut Tricks & Tips pdf with detailed solution & Short Tricks. So that you can easily get the logic of question. This Ratio & Proportion Short-Cut Tricks & Tips Pdf we are Providing is free to download. ” Most Important Ratio & Proportion Short-Cut Tricks & Tips Question PDF with Answers“
Ratio & Proportion Short-Cut Tricks & Tips Plays a vital role in Exam. In every exam you will get at least 5-10 questions from this topic. So candidates must focus on this topic and download this Ratio & Proportion Short-Cut Tricks & Tips pdf to get important questions with best solution regarding Ratio & Proportion Short-Cut Tricks & Tips. We have put all Previous Year Questions of Ratio & Proportion Short-Cut Tricks & Tips that are Asked in various Govt & Private Exam.
Ratio is a quantity which represents the relationship between two similar quantities. It expresses a magnitude by which quantity is multiple of another one. Ratio is represented as 2:3 or 2/3. Here, numerator i.e. 2 is known as “ANTECEDENT” and denominator i.e. 3 is known as “CONSEQUENT”.
If antecedent is more than the consequent, then it is known as improper ratio and if less ,then it is known as proper ratio.
RATIO:
Ratio can be simply said as fractions. A number which is written as a fraction. Then, the Ratio’s specified is not the exact value and it is the multiples of the value specified.
Ratio compares 2 numbers and they should be of the same unit
The reciprocal of the same number is not same ie (4/3) is not equal to(3/4)
Example:
| 4 The value is Multiples of 4 |
| 3 The value is Multiples of 3 |
# 1.TYPE 1:
BASIC PROBLEMS:
This is Basic type of questions in Ratio and Proportion,In this type Question contains Individual Ratio/Total Ratio and Individual Value/Total Value then,you will be asked to find the Ratio or Value.Since these type of questions are basic questions,and they can used in any other topic
1.If a certain sum of money is distributed among A and B in the ratio 4:3 and B gets Rs.3000,then what is total money distributed?
| A | B | A+B |
| 4x | 3x | 7x |
3x=3000 x=1000
Total money distributed =7x=7*1000=Rs.7000
2.If a certain task is distributed among A,B,C and D in the ratio 2:5:7:9 in 1 day then D performs 1800 task in 1 day. Then how many task is completed for 2day when A and B works?
D=9x=1800
x=200.
A and B when combines in 1 day they does = 2x+5x=7x
7*200=1400
For 2 days they complete 1400*2=2800 task.
# 2.TYPE 2:
BASED ON EFFICIENCY:
In this type efficiency of the Person is given and the ratio were also given we have to find the new ratio.Tricks and Tips to solve the Problem based on Efficiency.
1.Seats for mathematics, physics and biology in a school are in the ratio 5:7:8.There is a proposal to increase these seats by 40%,50% and 75% respectively. What will be the ratio of increased seats?
The ratio’s are 5x:7x:8x let x=10 then,
Mathematics=50 Physics =70 Biology=80
Then Increased Percentage be 40%,50% and 75%:
10% of 50=5 then 140% of 50=70
10% of 70=7 then 150% 0f 70=105
10%of 80=8 then 175% of 80=140
Mathematics=70 Physics =105 Biology=140
Their increased ratio=2:3:4
# 3.TYPE 3:
FORMATION OF NEW RATIO’S:
This type of Problem consists of two Ratio’s and we asked to find a new ratio.These type of questions can be asked in Ratio & Proportion Problems
1.If a_b=2:3 and b_c=2:4 then a:b:c=?
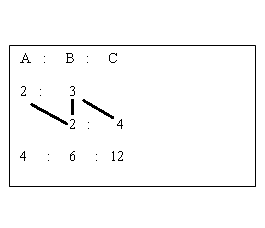
Therefore the new Ratio=2:3:6
2.If a_b=2:3 and b_c= 2:4 and c_d= 4:2 then a:b:c:d=?
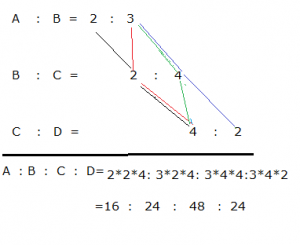
Therefore,the new Ratio is 2:3:6:3
PROPORTIONS:
The Equality Of Two Ratios Is Called Proportions.
Proportion has basically 5 types,Questions asked in IBPS Exams are nowadays with high difficulty,So, to solve all the difficult problem we should know how to solve the basic problems.Here we have covered all the basic Problem and its types and Shortcut method for solving all the basic Problems
That is:
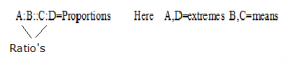
Rule:
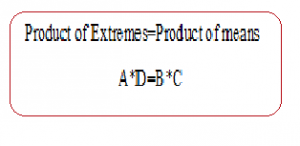
If X=KY, K=constant then X is directly proportional toY
XY=K, then X is inversely proportional to Y.
#.1.TYPE 1:
FINDING NUMBER OF PERSON:
These type of question in Proportionality are the basic type and we can solve these type of problems by two methods
1.Method 1:Solving by equations
2.Method 2:Shortcut Method
1.A Sum Of Rs.312 Is To Be Distributed Among 100 Boys And Girls Such That If Each Boy Gets Rs.3.60 And Each Girl Gets Rs.2.40 Then Find How Many Number Of Boys In The Class?
Let there be X boys in the class and Y girls in the girls
X+Y=100
3.6X+2.4Y=312
By solving 1 & 2 we get X=60 and Y=40
The number of boys present in the class=60
Shortcut Method:
| Boys | Girls |
| 3.60 | 2.40 |
| 3 | 2 |
100*(3/5)=60.The number of Boys=60
#.2 TYPE 2:
BASED ON ADDITION/SUBTRACTION OF QUANTITY:
1In A 80 Litre Of Solution Containing Milk And Water In The Ratio 2:3.How Much Milk Should Be Added To The Solution So That The New Ratio Becomes 4:1?
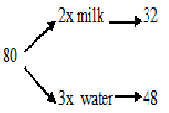
The new ratio is 4:1 that means only water is added to the solution which means that the water in the solution remains constant in the new ratio also
Therefore 1x=48litre
4x=192 litre where as the solution already contain 32 litre therefore we should add 160litres of milk
2.In A 60 Litres Mixture Of Milk And Water The Ratio Of Milk And Water Is 7:5.How Much Water Should Be Added In The Mixture So That The Ratio Of Milk To Water Becomes 5:7?
| Mixture 60 | |
| Milk | Water |
| 7x=35 | 5x=25 |
Milk is not added and kept as it is so 5x=35 x=7 there by 7x=7*7=49
Already there is 25litres of water in the mixture so additionally we need to add 24 litres of water
#.3 TYPE 3:
BASED ON EQUALITY:
If the original ratio a:b
Duplicate Ratio:a²:b²
Sub Duplicate Ratio: √a:√b
Triplicate Ratio: a³:b³
Sub Triplicate Ratio:a^(1/3):b^(1/3)
1.If Twice A Is Equal To 3b And That Is Equal To 5 Times Of C.Then Find A:b:c?
LCM of 2,3,5=30
a:b:c=30/2:30/3:30/5
=15:10:6
2.If The Sub Duplicate Ratio Of A_b=2:3.Then Find The Triplicate Ratio Of A:b?
√a:√b=2/3
a:b=4/9
a³:b³=64/729
3.A Hound Pursues A Hare And Takes 6 Leaps Foe Every 9 Leaps Of The Hare,But 3 Leaps Of The Hound Are Equal To 5leaps Of The Hare.Compare The Rates Of The Hound And The Hare?
Given:
| Hound | Hare |
| 6L | 9L |
3Hound=5Hare
Hound=(5/3)Hare
Rates of Hound:Rates of Hare
6*(5/3)L : 9L
10:9
Some important points:
1) If ratio is written as A:B, it is said to be a linear form and in case it is written as A/B, it is said to be fractional form.
2) Ratio does not have any unit. It is mere number.
3) The equality of two ratios is known as proportion i.e. a/b = c/d
If a/b = c/d , then it is also equal to a+c/b+d
Invertendo : If a/b = c/d , then b/a = d/c
Alterendo : If a/b = c/d , then a/c = b/d
Componendo : If a/b = c/d , then a+b/b = c+d/d
Dividendo : If a/b = c/d , then a-b/b = c-d/d
Componendo and Dividendo : If a/b = c/d , then a+b/a-b = c+d/c-d
4) If a/b = b/c = c/d =…… so on, then a,b,c,d… are in G.P.
Proof: Let a/b = b/c = c/d =k
c= dk, b= ck, a= bk
Therefore, b= dk^2 and a= dk^2
All are in G.P.
5) If a>b and same positive number is added to each term, then ratio decreases.
For example: a/b = 4/3 = 1.3, If 2 is added to each term, then a/b = 4+2/3+2 = 6/5 = 1.2
Therefore, ratio decreases.
6) If a<b and same positive number is added to each term, then ratio increases.
For example: a/b = 3/4 = 0.7, If 2 is added to each term, then a/b = 3+2/4+2 = 5/6 = 0.8
Therefore, ratio increases.
7) If we multiply or divide any number, there will be no effect on ratio.
8) Let a:b is a ratio
a^2:b^2 is duplicate ratio of a:b
a^3:b^3 is triplicate ratio of a:b
a^1/2:b^1/2 is sub-duplicate ratio of a:b
a^1/3:b^1/3 is sub-triplicate ratio of a:b
9) Proportions i.e. a:b = c:d
a and d are known to be extremes
b and c are known to be means.
10) In a:b :: c:d, d is fourth proportional to a,b and c.
Ratio And Proportion Concept
Ratio – It is a way of comparing two numbers or quantities and showing the relationship between them.
It is denoted by → ‘:’
Ex: In a class, there are 60 boys and 40 girls. What is the ratio of boys and girls?
Sol.: boys=60 and girls=40
Ratio= boys/girls =60/40=3/2=3:2
3:2 means हर three boys पर 2 girls है | या मैं ऐसा भी बोल सकता हूँ कि 5(i.e 3+2=5) students में 3 boys है or 2 girls है|
→ If boys : girls = 3 : 2 क्या मैं ऐसा भी बोल सकता हूँ कि boys=3 or girls=2 तो मेरा Ans. है नहीं. क्योंकि मैंने common factor को cancel out कर दिया है उसके बाद हमे 3:2 प्राप्त हुआ है |
यदि हमे boys and girls का individual value निकलना हो तो common factor से multiply करना होगा |
that means boys=3×20=60 and girls=2×20=40.here common factor=20 यहाँ पर मुझे common factor मालूम था तो मैंने individual value निकाल लिया |
यदि मुझे common factor मालूम नहीं होता तो मैं boys=3x and girls=2x लिखता|
Ex: In a class, the ratio of boys and girls is 3:2. If there are total 100 students, then how many boys and girls in the class.
Solution:
Let boys=3x and girls=2x
Now,
5x=100
x=20
so,boys=3x=3×20=60and girls=2x=2×20=40
Another way:
In 5 (i.e 3+2=5) students there are 3 boys
so, 1 student, there are 3/5 boys
∴ In 100 student boys are=(3/5)×100=60 boys
In 5 (i.e 3+2=5) students there are 2 girls
so, 1 student, there are 2/5 girls
∴ In 100 student girls are=(2/5)×100=40 girls
OR
girls=100-60=40 girls
Shortcut:
boys=(3/5)×100=60 boys
Girls=(2/5)×100=40 girls
Important Point:
⇒ For a ratio, the two quantities must be in the same unit.
Ex: Ratio of Rs 5 to Rs 30 here unit=Rs. In this example both quantities unit are same.
So, Ratio=5/30=1:6
Ex-2 Ratio of Rs 5 to 30 paise.
Solution: we can’t express in the form of a ratio. because a unit of both quantities is not same.
if u want to express in the form of a ratio, first of all, make the unit of both quantities are same ie. Rs 5 to Rs 0.30 or 500 paise to 30 paise.
Rule:
The multiplication or division of each term of a ratio by the same non-zero number does not effect the ratio.
Ex: 4:5

PROPORTION:
If the ratio of the first and second quantities is equal to the ratio of the third and fourth quantities then it is called proportion.
It is represented by → ‘::’
i.e if a_b=c:d, we write a:b::c:d and we say that a, b, c, d are in proportional
Here a and d are called extremes while b and c are called mean terms.
Ex: check 6, 10, 48, 80 are in proportional
Solution: 6/10=3/5=3:5
and 48/80=3/5=3:5
so, 6, 10, 48, 80 are in proportional.
⇒ Fourth Proportional: If a_b=c:d, then d is called the fourth proportional to a, b, c.
⇒Fourth Proportional(d) =(b×c)/a
⇒ Third Proportional: If a_b=b:c, then c is called the third proportional to a and b.
⇒Third Proportional(c)=b²/a
⇒Mean Proportional between a and b= √ab.
⇒Duplicate ratio of a_b= a²:b² .
⇒Sub-duplicate ratio of a_b= √a:√b .
⇒Triplicate ratio of a:b = a³:b³
A common type of Ratio And Proportion problem that is frequently asked in the various competitive exam.
(Q1)If A_B=2:3 B_C=4:3 Find A:B:C
Solution:
[Concept: A:B and B:C दोनों में B common है so दोनों में जो B का ratio दिया हुआ है उसे equal करेंगें|]

∴ A:B:C=8:12:9 Ans.
2nd Method:

∴ A:B:C=8:12:9 Ans.
(Q2) A_B=2:1 and A_C=1:3 then A:B:C is
Solution:
[Concept: A:B and A:C दोनों में A common है so दोनों में जो A का ratio दिया हुआ है उसे equal करेंगें|]

∴ A:B:C=2:1:6 Ans.
(Q3)If A_B=5:2 B_C=2:3 C_D=5:3 find ratio of A:B:C:D=?
Solution:

[Concept: A:B:C and C:D दोनों में C common है so दोनों में जो C का ratio दिया हुआ है उसे equal करने के लिए 5 से multiply किया गया है|]
(Q4)If A_B=4:9 and A_C=2:3 then (A+B):(A+C) is.
Solution:
[Concept: A:B and A:C दोनों में A common है so दोनों में जो A का ratio दिया हुआ है उसे equal करेंगें|]

∴ A:B:C=4:9:6
Now,
(A+B):(A+C)=(4+9):(4+6)=13:10 Ans.
(Q5)If 2A=3B=4C, then A:B:C is.
Solution:
L.C.M of 2,3,4=12
Now,
2A/12 =3B/12 = 4C/12
A/6 = B/4 = C/3
A:B:C=6:4:3 Ans.
(Q6)If A=(1/4)B and B=(½)C then A:B:C is
Solution:
A/B=1/4 and B/C=1/2
A:B=1:4 and B_C=1:2
[Concept: A:B and B:C दोनों में B common है so दोनों में जो B का ratio दिया हुआ है उसे equal करेंगें|]

So, A:B:C=1:4:8 Ans.
(Q7)If A_B=2:3 and B_C=3:7 then (A+B):(B+C):(C+A) is.
Solution:
[Concept: A:B=2:3 B:C=3:7 दोनों में B common है so दोनों में जो B का ratio दिया हुआ है उसे equal करेंगें| but in this question ratio of B in both cases are equal.]
∴ A:B:C=2:3:7
So, (A+B):(B+C):(C+A)=5:10:9 Ans.
(Q8)If x_y=4:5 then (3x+4y):(5x+3y)=?
Solution:
x:y=4:5
x/y=4/5

Put the value of x/y then
(3x+4y):(5x+3y)=17:35 Ans.
(Q9)If a:b:c=2:3:4 and 2a-3b+4c=33, then the value of c is.
Solution:
a:b:c=2:3:4
∴ a/2 = b/3 = c/4 = K(let)
⇒ a=2k, b=3k, and c=4k
Given that 2a-3b+4c=33
=>2×2k-3×3k+4×4k=33
so, k=3
∴ c=4k=4×3=12 Ans.
(Q10)The fourth proportional to 4, 9, 12 is.
Solution:
Let the fourth proportional to 4, 9, 12 be x.
then 4:9::12:x
⇒4×x=9×12 (i.e a×d=b×c)
∴ x=27 Ans.
(Q11)The third proportional to 16 and 36 is.
Solution:
Let the third proportional to 16 and 36 be x
then 16:36:36:x
⇒ 16×x=36×36
∴ x=81 Ans.
(Q12)The mean proportional between 0.08 and 0.18 is.
Solution:
The mean proportional between 0.08 and 0.18=

Ratio And Proportion Problem with solution and Shortcut Tricks Type-2
(Q1)The product of two positive integers is 1575 and their ratio is 9:7. The smaller integer is.
दो संख्याओं का गुणनफल 1575 है और उनका अनुपात 9:7 है तो छोटी संख्या ज्ञात करें|
Solution:
Let the integers be 9x and 7x respectively
According to question
9x×7x = 1575
⇒ x² = 1575/63=25
⇒ x= 5
∴ smaller integer=7x=7×5=35 Ans.
(Q2)Three numbers are in the ratio of 3:2:5 and the sum of their squares are 1862. The smallest of these number is.
तीन संख्याओं का अनुपात 3:2:5 है और उनके वर्गो का योग 1862 है, तो सबसे छोटी संख्या ज्ञात करें|
Solution:
Let the number be 3x, 2x and 5x respectively
According to question
(3x)² + (2x)² + (5x)² = 1862
⇒38x²=1862
⇒x²=1862/38=49
⇒x = 7
∴ The smallest number=2x=2×7=14 Ans.
(Q3)The sum of three numbers is 116. The ratio of second to the third is 9:16 and the first to the third are 1:4. The second number is.
तीन संख्याओं का योग 116 है| दूसरी और तीसरी संख्या का अनुपात 9:16 और पहली और तीसरी संख्या का अनुपात 1:4 है, तो दूसरी संख्या ज्ञात करें|
Solution:

Therefore, the second number=(9/29)×116
= 36 Ans.
(Q4)Of the three numbers, the ratio of the first and the second is 8:9 and that of the second and third is 3:4. If the product of the first and third number is 2400, then the second number is:
तीन संख्याओं में पहली और दूसरी संख्याओं का अनुपात 8:9 है और दूसरी व तीसरी का अनुपात 3:4 है| यदि पहली और तीसरी का गुणनफल 2400 है, तो दूसरी संख्या ज्ञात करें|
Solution:

Let the 1st, 2nd, and 3rd number be 8x, 9x, and 12x respectively
8x×12x=2400
⇒ x²=2400/96 = 25
⇒ x=5
2nd number=9x=9×5=45 Ans.
(Q5)what number should be added to each of 6, 14, 18 and 38 so that the resulting numbers make a proportion?
किस संख्या को 6, 14, 18, तथा 38 प्रत्येक में जोड़ा जाए की नई संख्याएँ समानुपातिक हो जाए|
Option: (1) 3 (2) 2 (3) 4 (4) 1
Solution:
Concept: if a, b, c, d are in proportion then a:b::c:d or a_b=c:d or a/b = c/d
Let x is added then
(6+x)/(14+x) = (18+x)/(38+x)
⇒ 228+38x+6x+x² = 252+14x+18x+x²
⇒ x²+44x+228 = x²+32x+252
⇒ 12x=24
∴x=2 Ans.
Second Method:
Let x is added then
(6+x)/(14+x) = (18+x)/(38+x)
put the value from option then
(6+2)/(14+2) = (18+2)/(38+2)
⇒ 8/16 = 20/40
⇒ 1/2 = 1/2
(Q6)Three numbers are in the ratio 3:4:5. The sum of the largest and the smallest equals the sum of the second and 52. the smallest number is.
तीन संख्याएँ 3:4:5 अनुपात में है| यदि सबसे बड़ी व सबसे छोटी संख्याओं का योग दूसरी संख्या व 52 के योग के बराबर है तो सबसे छोटी संख्या ज्ञात करें|
Solution:
Let the numbers be 3x, 4x and 5x
Now according to question
5x+3x = 4x+52
⇒ 4x=52
⇒ x=13
∴ Smallest number=3x=3×13=39 Ans.
(Q7)If the square of the sum of two numbers is equal to 4 times of their product, then the ratio of these numbers is:
किन्ही दो संख्याओं के योग का वर्ग, उनके गुणनफल के चार गुने के बराबर है, तो संख्याओं का अनुपात क्या है |
Solution:
Let the numbers are x and y
Now according to question
(X+y)² = 4xy
⇒ x² + y²+2xy = 4xy
⇒ x² + y²-2xy=0
⇒ (x-y)² = 0
so, x=y
∴ x_y=1:1 Ans.
(Q8)The sum of two numbers is equal to 20 and their difference is 25. The ratio of the two numbers is.
दो संख्याओं का योग 20 है और उनका अंतर 25 है तो संख्याओं का अनुपात ज्ञात करें|
Solution:
1st method: Shortcut
20+25 : 20-25
=45 : 5
=9 : 1 Ans.
2nd Method: General
Let the numbers are x and y
Now according to question
x+y = 25 ← (1)
x-y = 20 ← (2)
on adding Eqn.(1)and (2)
⇒ 2x= 45
⇒ x=22.5
put the value of x in Eqn.(1)
⇒ 22.5+y=25
y=2.5
∴ Required ratio=22.5:2.5 =9:1 Ans
(Q9)If A and B are in the ratio 4:5 and the difference of their squares is 81, what is the value of A?
यदि A तथा B 4:5 के अनुपात में है और उनके वर्गो का अंतर 81 है, तो A का मान ज्ञात करें|
Solution:
Let A=4x and B=5x
Now according to question
(5x)² – (4x)² = 81
⇒ 9x² =81
⇒ x² =81/9 = 9
⇒ x= 3
∴ A=4x=4×3=12 Ans.
Ratio And Proportion Problem with solution and Shortcut Tricks for SSC, Bank PO, Railway, Lic Exam Type-2.1
(Q1)The ratio of two numbers is 3:4 and their LCM is 120. The sum of numbers is.
दो संख्याएँ 3:4 के अनुपात में है और उनका लघुत्तम समापवर्त्य 120 है तो संख्याओं का योग ज्ञात करें|
Solution:
Let the numbers be 3x and 4x respectively.
LCM of 3x and 4x=12x
⇒ 12x=120
⇒ x=10
∴ Sum of the numbers=3x+4x=7x=7×10=70 Ans.
(Q2)The ratio of two numbers is 3:4 and their HCF is 15. Then the sum of the two numbers is:
दो संख्याएँ 3:4 के अनुपात में है और उनका महत्तम समापवर्त्य 15 है तो संख्याओं का योग ज्ञात करें|
Solution:
Let the numbers be 3x and 4x respectively.
HCF of 3x and 4x=x
⇒ x=15
∴ Sum of the two numbers=3x+4x=7x=7×15=105 Ans.
Ratio And Proportion Problem with solution and Shortcut Tricks for SSC, Bank PO, Railway, Lic Exam Type-2.2
(Q1)In a school having roll strength 286, the ratio of boys and girls is 8:5. If 22 more girls get admitted into the school, the ratio of boys and girls becomes.
286 छात्रों की एक स्कूल में लड़कों व लड़कियों का अनुपात 8:5 है| यदि 22 और लड़कीयाँ स्कूल में दाखिला लेती है तो लड़कों व लड़कियों का नया अनुपात ज्ञात करें |
Solution:
Let boys=8x and girls=5x
Now, According to the question
8x+5x=286
⇒ x= 286/13 =22
Boys=8×22=176
Girls=5×22=110
No. of girls at present after adding 22 girls=110+22=132
∴ Ratio=176/132=4:3 Ans.
Method-2
Initially number of boys=(8/8+5)×286=(8/13)×286=176
Number of girls=(5/13)×286=110
No. of girls at present after adding 22 girls=110+22=132
∴ Ratio=176/132=4:3 Ans.
(Q2)If there is a reduction in the number of workers in a factory in the ratio 15:11 and an increment in their wage in the ratio 22:25, then the ratio by which the total wage of the workers should be decreased is.
यदि एक कारखाने में मजदूरों की संख्या में 15:11 के अनुपात में कटौती हो और उनकी मजदूरी 22:25 के अनुपात में बढाई जाए तो उनकी कुल घटी हुई मजदूरी का अनुपात ज्ञात करें |
Solution:

(Q3)Two numbers are in the ratio 3:5. By adding 10 to each of them, the new numbers are in the ratio 5:7. Find the two numbers.
दो संख्याओ का अनुपात 3:5 है| यदि प्रत्येक संख्या में 10 जोड़ दी जाए तो उनका अनुपात 5:7 हो जाता है, तो संख्याएँ ज्ञात करें |
Solution: 1st Method: Shortcut

Now,
2 unit = 10
1 unit = 5
1st number=3×5=15
2nd number=5×5=25
Second Method: Shortcut

Now, cross multiply
(25-21)/7-5 = 4/2=2
Concept:[ 2 unit को 10 unit बनाना होगा क्योंकि question में दिया है 10 unit add किया जा रहा है |]
So, 2×5=10
1st number=3×5=15
2nd number=5×5=25
Third Method: General Method
Let the number be 3x and 5x
Now, According to the question
(3x+10)/(5x+10) = 5/7
⇒2x+70 = 25x+50
⇒4x=20
∴ x=5
1st number=3×5=15
2nd number=5×5=25
Important Note:जब difference same आएगा तब हमलोग इस type के question को method-1,2 and 3 किसी भी method से solve कर सकते है पर यदि इस type के question में difference same नहीं आएगा तब हमलोग method-2 and 3 से solve करेंगे|
(Q4)What should be added to each term of the ratio 7:11, so as to make it equal to 3:4?
7:11 अनुपात की प्रत्येक संख्या में किस संख्या को जोड़ा जाए की अनुपात 3:4 हो जाए|
Solution: 1st Method: Shortcut

Now, cross multiply
(33-28)/4-3 = 5/1=5 Ans.
2 nd Method: General Method
Let the required number be x.
Now,
(7+x)/(11+x)= 3/4
⇒28+4x = 33+3x
⇒ x= 5 Ans.
(Q5)Two numbers are in the ratio 4:5 respectively. If each number is subtracted by 25, then the ratio becomes 3:4. Find the two numbers.
दो संख्याओ का अनुपात 4:5 है| यदि प्रत्येक संख्या में से 25 घटा दी जाए तो उनका अनुपात 3:4 हो जाता है, तो संख्याएँ ज्ञात करें |
Solution:1st Method: Shortcut

Now
1 unit = 25
1st number=4×25=100
2nd number=5×25=125
Second Method: Shortcut

Now, cross multiply
(16-15)/4-3 = 1/1=1
Concept:[ 1 unit को 25 unit बनाना होगा क्योंकि question में दिया है 25 unit subtract किया जा रहा है |]
So, 1×25=25
1st number=4×25=100
2nd number=5×25=125
Third Method: General Method
Let the number be 4x and 5x
Now, According to the question
(4x-25)/(5x-25) = 3/4
⇒16x-100 = 15x-75
⇒x=25
1st number=4×25=100
2nd number=5×25=125
Important Note:जब difference same आएगा तब हमलोग इस type के question को method-1,2 and 3 किसी भी method से solve कर सकते है पर यदि इस type के question में difference same नहीं आएगा तब हमलोग method-2 and 3 से solve करेंगे|
(Q6)What number should be subtracted from both the terms of the ratio 11:15 so as to make it as 2:3?
11:15 अनुपात की संख्याओ में किस संख्या को घटाया जाए की अनुपात 2:3 हो जाए|
Solution:1st Method: Shortcut

Now, cross multiply
(33-30)/3-2 = 3/1=3 Ans.
2 nd Method: General Method
Let the required number be x.
Now,
(11-x)/(15-x)= 2/3
⇒33-3x = 30-2x
⇒ x= 3 Ans.
(Q7)The students in three classes are in the ratio 4:6:9. If 12 students are increased in each class, the ratio changes to 7:9:12. Then the total number of students in the three classes before the increase is.
तीन कक्षाओं में छात्रों का अनुपात 4:6:9 है | यदि प्रत्येक कक्षा में 12 छात्र बढ़ा दी जाए तो अनुपात 7:9:12 हो जाता है, तो शुरुआत में कुल कितने छात्र थे |
Solution:1st Method: Shortcut

Now,
3 unit=12
1 unit=4
Initially the number of students=19 unit=19×4=76 Ans.
2 nd Method: General Method
Let the original number of student be 4x, 6x, and 9x
Now,
(4x+12)/(6x+12)=7/9
⇒ 42x+84 = 36x+108
⇒ 6x= 24
⇒ x= 4
Initially the number of students=19x=19×4=76 Ans.
Important Note:जब difference same आएगा तब हमलोग इस type के question को method-1 and 2 किसी भी method से solve कर सकते है पर यदि इस type के question में difference same नहीं आएगा तब हमलोग method-2 से solve करेंगे|
(Q8)The ratio between the boys and girls in a class is 6:5 respectively. If 8 more boys join the class and two girls leave the class then the respective ratio becomes 11:7. What is the number of boys in the class now?
एक कक्षा में लड़के व लड़कियों का अनुपात क्रमशः 6:5 है| यदि 8 और लड़के कक्षा में दाखिला लेता है एवं 2 लड़कीयाँ कक्षा छोड़ती है तो लड़के व लड़कियों का अनुपात 11 :7 हो जाता है तो अभी कक्षा में लडको कि संख्या क्या है |
Solution:
Let the number of boys and girls be 6x and 5x respectively.
According to the question,
(6x+8)/(5x-2) = 11/7
⇒42x+56=55x-22
⇒13x=78
⇒x=6
∴ Number of boys in the class=6x+8
=6×6+8=42 Ans.
Ratio And Proportion Problem Shortcut Tricks Type-3
(Q1)80 liters of a mixture contains milk and water in the ratio of 27:5. How much is more water to be added to get a mixture containing milk and water in the ratio of 3:1?
80 लीटर के एक मिश्रण में दूध व पानी का अनुपात 27:5 है | तो कितना पानी और मिलाया जाए की मिश्रण में दूध व पानी का अनुपात 3:1 हो जाए|
Solution: Method-1-Shortcut

[Concept: According to question mixture में अलग से only water add करने की बात की जा रही है so in both situation(i.e initial state and Final state) quantity of milk will be equal. but यहाँ पर milk की मात्रा(quantity) दोनों में equal नहीं है so milk की मात्रा(quantity) equal करनी होगी| ]

32units(i.e 27+5)=80 litres
1 unit=80/32
∴ 4 unit=(80/32)×4=10 litres Ans.
Method-2

Milk(M)=80×(27/32)=67.5 litres
Water(W)=80×(5/32)=12.5 litres
OR
Water=80-67.5=12.5 litres
Now,
Let x litre water to be added then
67.5/(12.5+x)=3/1
⇒ 37.5+3x=67.5
∴ x=10 litre Ans.
Method-3
Let quantity of milk in the mixture=27x
and quantity of water =5x
Now,
32x=80 liters
∴ x=5/2
Milk=27x=27×(5/2)=67.5 litres
Water=5x=5×(5/2)=12.5 litres
Let y litre water to be added then
67.5/(12.5+y)=3/1
⇒ 37.5+3y=67.5
∴ y=10 litre Ans.
(Q2)20 litres of a mixture contains milk and water in the ratio of 3:1. How much more milk is to be added to get a mixture containing milk and water in the ratio of 4:1?
20 लीटर के एक मिश्रण में दूध व पानी का अनुपात 3:1 है | तो कितना दूधऔर मिलाया जाए की मिश्रण में दूध व पानी का अनुपात 4:1 हो जाए|
Solution: Method-1: Shortcut

[Concept: According to question mixture में अलग से only milk add करने की बात की जा रही है so in both situation(i.e initial state and Final state) quantity of water will be equal. but यहाँ पर water की मात्रा(quantity) दोनों में पहले से equal है so water की मात्रा(quantity) equal करने की जरूरत नहीं है| ]
So,

4 unit(i.e 3+1)=20 liters
∴ 1 unit=20/4=5 litres Ans.
Method-2

Milk(M)=20×(3/4)=15 liters
Water(W)=20×(1/4)=5 liters
OR
Water=20-15=5 liters
Now,
Let x litre milk to be added then
(15+x)/(5)=4/1
⇒ 15+x=20
∴ x=5 litre Ans.
(Q3)729 ml of a mixture contains milk and water in the ratio 7:2. How much more water is to be added to get a new mixture containing milk and water in the ratio 7:3?
729 ml के एक मिश्रण में दूध व पानी का अनुपात 7:2 है | तो कितना पानी और मिलाया जाए की मिश्रण में दूध व पानी का अनुपात 7:3 हो जाए|
Solution: Shortcut

[Concept: According to question mixture में अलग से only water add करने की बात की जा रही है so in both situation(i.e initial state and Final state) quantity of milk will be equal. but यहाँ पर milk की मात्रा(quantity) दोनों में पहले से equal है so milk की मात्रा(quantity) equal करने की जरूरत नहीं है| ]
So,

9 unit(i.e 7+2)=729
∴ 1 unit=729/9=81 ml Ans.
(Q4)An alloy contains copper, zinc, and nickel in the ratio of 5:3:2. The quantity of nickel (in Kg) that must be added to 100 kg of this alloy to have the new ratio 5:3:3 is.
एक मिश्रधातु में तांबा, जिंक तथा निकेल 5:3:2 के अनुपात में है| इस मिश्रधातु के 100 kg में कितनी निकेल की मात्रा (किग्रा. में ) डाली जाए की नया अनुपात 5:3:3 हो जाए|
Solution: Shortcut

10 unit(i.e 5+3+2)=100 kg
∴ 1 unit=100/10=10 Kg Ans.
Ratio And Proportion Problem Shortcut Tricks for Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-3.1
(Q1)A mixture contains milk and water in the ratio 5:2 on adding 22 litres of water, the ratio of milk and water becomes 7:5. The quantity of water in the original mixture is.
एक मिश्रण में दूध व पानी का अनुपात 5:2 है| यदि 22 लीटर पानी और मिलाया जाए तो नए मिश्रण में दूध व पानी काअनुपात 7:5 हो जाता है तो original मिश्रण में पानी की कुल मात्रा ज्ञात करे|
Solution: Shortcut

[Concept: According to question mixture में अलग से 22 litres water add करने की बात की जा रही है so in both situation(i.e initial state and Final state) quantity of milk will be equal. but यहाँ पर milk की मात्रा(quantity) दोनों में equal नहीं है so milk की मात्रा(quantity) equal करनी होगी| ]

11 unit=22 liters
1 unit=22/11
∴ 14 unit=(22/11)×14=28 liters Ans.
Method-2
Let the initial quantity of milk in mixture=5x and water=2x
adding 22 liters of water then
5x/(2x+22)=7/5
25x=14x+154
∴ x=14
The quantity of water in the original mixture=2x=2×14=28 liters Ans.
(Q2)The milk and water in a mixture are in the ratio 7:5. When 15 litres of water are added to it, the ratio of milk and water in the new mixture becomes 7:8. The total quantity of water in the new mixture is.
एक मिश्रण में दूध व पानी का अनुपात 7:5 है| यदि 15 लीटर पानी और मिलाया जाए तो नए मिश्रण में दूध व पानी काअनुपात 7:8 हो जाता है तो नए मिश्रण में पानी की कुल मात्रा ज्ञात करे|
Solution: Shortcut

[Concept: According to question mixture में अलग से 15 litres water add करने की बात की जा रही है so in both situation(i.e initial state and Final state) quantity of milk will be equal. but यहाँ पर milk की मात्रा(quantity) दोनों में पहले से equal है so milk की मात्रा(quantity) equal करने की जरूरत नहीं है| ]
Now,

3 unit=15
1 unit=15/3
∴ 8 unit=(15/3)×8=40 litre Ans.
Method-2
Let the initial quantity of milk in mixture=7x and water=5x
adding 15 liters of water then
7x/(5x+15)=7/8
56x=35x+105
∴ x=5
In new mixture milk=7x and water=8x
The quantity of water in the new mixture=8x=8×5=40 liters Ans.
(Q3)The milk and water in a mixture is 1:3. If 5 litres of milk are added to it, the ratio of milk and water in the new mixture becomes 1:2. The total quantity of new mixture(in litres) is.
एक मिश्रण में दूध व पानी का अनुपात 1:3 है| यदि 5 लीटर दूध और मिलाया जाए तो नए मिश्रण में दूध व पानी का अनुपात 1:2 हो जाता है तो नए मिश्रण की कुल मात्रा ज्ञात करे|
Solution: Shortcut

[Concept: According to question mixture में अलग से 5 litres milk add करने की बात की जा रही है so in both situation(i.e initial state and Final state) quantity of water will be equal. but यहाँ पर water की मात्रा(quantity) दोनों में equal नहीं है so water की मात्रा(quantity) equal करनी होगी| ]
Now,

1 unit=5 litres
9 unit(i.e3+6)=9×5=45 litres Ans.
Method-2
Let the initial quantity of milk in mixture=x and water=3x
adding 5 liters of milk then
(x+5)/3x=1/2
⇒2x+10=3x
⇒x=10
∴ quantity of new mixture=4x+5
=4×10+5=45 liters Ans.
(Q4)In a mixture of 25 litres, the ratio of acid to water is 4:1. Another 3 litres of water is added to the mixture. The ratio of acid to water in the new mixture is.
25 लीटर के एक मिश्रण में एसिड व पानी का अनुपात 4:1 है | यदि मिश्रण में 3 लीटर पानी मिलाया जाए, तो नए मिश्रण में एसिड व पानी का अनुपात क्या होगा|
Solution:

Acid= 25×(4/5)=20 litres
Water=25-20=5 litres
After adding 3 liters of water then total quantity of water=5+3=8 liters
Now, Ratio=20/8=5:2 Ans
Method-2
Let the initial quantity of Acid in mixture=4x and water=x
now,
5x(i.e 4x+x=5x)=25
⇒ x=5
Acid=4x=4×5=20 liters
Water=x=5 liters
after adding 3 liters of water then total quantity of water=8 liters
Now, ratio=20/8=5:2 Ans.
Ratio And Proportion Problem Shortcut Tricks for Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-3.2
(Q1)Two equal vessels are filled with the mixture of milk and water in the ratio of 3:2 and 4:1 respectively. If the mixture is poured into a third vessel, the ratio of milk and water in the third vessel will be.
दो पतीला समान क्षमता के है जिसमे दूध व पानी के मिश्रण का अनुपात क्रमश: 3:2 और 4:1 है| यदि दोनों मिश्रण को तीसरा पतीला में मिला दिया जाए तो तीसरा पतीला के मिश्रण दूध व पानी का अनुपात क्या होगा|
Solution: Shortcut

[Concept: If total quantity of both vessels are equal then add milk+milk : water+water ]
Here the quantity of both vessels are equal so, the ratio of milk and water in the third vessel=7:3 Ans.
Method-2
Total quantity of milk=(3/5)+(4/5)=7/5
Total quantity of water=(2/5)+(1/5)=3/5
Ratio=(7/5)/(3/5)=7:3 Ans.
(Q2)There are two containers of equal capacity. The ratio of milk to water in the first container is 3:1, in the second container 5:2. If they are mixed up, the ratio of milk to water in the mixture will be.
दो बर्तन समान क्षमता के है| पहले बर्तन में दूध व पानी का अनुपात 3:1 है और दूसरे बर्तन में दूध व पानी का अनुपात 5:2 है| यदि दोनों को मिला दिया जाए तो मिश्रण में दूध व पानी का अनुपात क्या होगा|
Solution:

[Concept: Here total quantity of both containers are not equal so first of all we will have to make a total quantity of both containers are equal. Total quantity ko equal करने के लिए जिस-जिस number से 1st and 2nd के total quantity को multiply किया जाएगा उसी-उसी number से उनके ratio को भी multiply करेंगे|]
Now,

Method-2
Total quantity of milk=(3/4)+(5/7)=41/28
Total quantity of water=(1/4)+(2/7)=15/28
Ratio=(41/28)/(15/28)=41:15 Ans.
(Q3)Three utensils contain equal quantity of mixtures of milk and water in the ratio 2:3, 1:4 and 4:1 respectively. If all the solutions are mixed together, the ratio of milk and water in the new mixture is.
तीन बर्तन समान क्षमता के है जिसमे दूध व पानी के मिश्रण का अनुपात क्रमश: 2:3, 1:4और 4:1 है|यदि तीनों बर्तन के मिश्रण को मिला दिया जाए तो नए मिश्रण में दूध व पानी का अनुपात क्या होगा|
Solution: Shortcut

Here total quantity of all utensils are equal, so ratio of milk and water =7:8 Ans
Concept: [Total quantity of all are equal then simply Add, (milk1+milk2+milk3) : (water1+water2+water3) ]
2nd method:
Total quantity of milk=2/5+1/5+4/5=7/5
Total quantity of water=3/5+4/5+1/5=8/5
Ratio= (7/5)/(8/5) = 7:8 Ans.
(Q4)Three glasses of equal volume contains acid mixed with water. The ratios of acid and water are 6:1, 5:2 and 3:1 respectively. Contents of these glasses are poured in a large vessel. The ratio of acid and water in the large vessel is.
तीन ग्लास समान क्षमता के है जिसमे पानी से मिला एसिड रखा गया है | एसिड व पानी का अनुपात क्रमश: 6:1, 5:2और 3:1 है|यदि तीनों ग्लासों के मिश्रण को एक टब में मिला दिया जाए तो इस मिश्रण में एसिड व पानी का अनुपात क्या होगा|
Solution:

[Concept: Here total quantity of all glass are not equal so first of all we will have to make a total quantity of all glass are equal. Total quantity को equal करने के लिए जिस-जिस number से 1st and 2nd and 3rd के total quantity को multiply किया जाएगा उसी-उसी number से उनके ratio को भी multiply करेंगे|]
Now,

2nd Method
Total acid= (6/7)+(5/7)+(3/4)
= (24+20+21)/28 = 65/28
Total water= (1/7)+(2/7)+(1/4)
= (4+8+7)/28 = 19/28
∴ Ratio= (65/28)/(19/28) = 65:19 Ans.
Ratio And Proportion Problems And Solutions Type-4
(Q1) Two container A and B contain a mixture of Acid and water in the ratio of 4:5 and 5:1. If both containers are mixed in the proportion of 5:2 respectively, Find the ratio of acid and water in the newly formed mixture is.
दो बर्तन A और B में एसिड और पानी का मिश्रण रखा गया है जिसमें एसिड और पानी का अनुपात 4:5 और 5:1 है| यदि दोनों बर्तन को 5:2 के अनुपात में मिलाया जाता है तो नए मिश्रण में एसिड और पानी का अनुपात क्या होगा|
Solution:

In 5 unit of mixture
Quantity of acid=(4/9)×5=20/9
Quantity of water=(5/9)×5=25/9
In 2 unit of mixture
Quantity of acid=(5/6)×2=5/3
Quantity of water=(1/6)×2=1/3
∴ Required ratio=[(20/9)+(5/3) : (25/9)+(1/3)]
= 35/9:28/9 =5:4 Ans.
Second Method:

[ Concept: Container A और container B का total quantity equal नहीं है so,Step-1: Container A और container B के total quantity को equal करना है| equal करने के लिए जिस number से total quantity को multiply किया जाएगा उसी- उसी number से उसके ratio को भी multiply करना है| Step-2: दोनों container को जिस ratio में मिलाया जा रहा है फिर उससे multiply करना है ]

(Q2) Two alloys contain tin and iron in the ratio of 1:2 and 2:3. If the two alloys are mixed in the proportion of 3:4 respectively the ratio of tin and iron in the newly formed alloy is:
दो मिश्र धातुओं में टीन तथा लोहा 1:2 और 2:3 के अनुपात में है| यदि मिश्र धातुओं को 3:4 के अनुपात में मिलाया जाता है, तो नए मिश्र धातु में टीन तथा लोहे का अनुपात क्या होगा|
Solution:

[ Concept: 1st alloy और 2nd alloy का total quantity equal नहीं है so,Step-1: 1st alloy और 2nd alloy के total quantity को equal करना है| equal करने के लिए जिस number से total quantity को multiply किया जाएगा उसी- उसी number से उसके ratio को भी multiply करना है| Step-2: दोनों container को जिस ratio में मिलाया जा रहा है फिर उससे multiply करना है ]

(Q3)Three glasses contains acid mixed with water. The ratios of acid and water are 3:2, 2:1 and 2:3 respectively. If the mixture taken out in the ratio 10:9:5. What is the ratio of acid and water in new mixture is.
तीन ग्लास जिसमे पानी से मिला एसिड रखा गया है | एसिड व पानी का अनुपात क्रमश: 3:2, 2:1और 2:3 है|यदि मिश्रण को 10:9:5 के अनुपात में निकला जाए तो नए मिश्रण में एसिड व पानी का अनुपात क्या होगा|
Solution:

[ Concept: 1st glass, 2nd glass और 3nd glass का total quantity equal नहीं है so, Step-1: 1st glass, 2nd glass और 3nd glass के total quantity को equal करना है| equal करने के लिए जिस number से total quantity को multiply किया जाएगा उसी- उसी number से उसके ratio को भी multiply करना है| Step-2: तीनों container से जिस ratio में मिश्रण निकाला जा रहा है फिर उससे multiply करना है ]

Ratio And Proportion Problems And Solutions for Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-4.1
(Q1)Two vessels contain milk and water in the ratio 3:5 and 6:1. Find the ratio in which the contents of the two vessels have to be mixed to get a new mixture in which the ratio of milk and water is 7:3.
दो बर्तन में दूध व पानी का मिश्रण 3:5 और 6:1 के अनुपात में है| तो इन्हें किस अनुपात में मिलाया जाए की नए मिश्रण में दूध व पानी का अनुपात 7:3 हो जाए|
Solution:

∴ Required ratio=(11/70):(13/40)
=44:91 Ans.
OR

∴ Required ratio=(11/70):(13/40)
=44:91 Ans.
(Q2)In two blends of mixed tea, the ratios of Darjeeling and Assam tea are 4:7 and 2:5. The ratio in which these two blends should be mixed to get the ratio of Darjeeling and Assam tea in the new mixture as 6:13 is.
मिश्रित चाय के दो मिश्रणों में दार्जीलिंग और असम चाय के अनुपात 4:7 और 2:5 है| इन दोनों मिश्रणों को किस अनुपात में मिलाया जाए कि दार्जिलिंग और असम चाय का अनुपात नए मिश्रण में 6:13 हो जाए|

∴ Required ratio=(4/(19×7)):(10/(11×19))
=22:35 Ans.
OR

∴ Required ratio=(4/(7×19)):(10/(19×11))
=22:35 Ans.
Ratio And Proportion Problems And Solutions for Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-4.2
(Q1)A vessel contains 80 liters of milk. 8 liters of milk is taken out from it and replaced by water. Then again from mixture, 8 liters is again taken out and replaced by water. Find the amount of milk in the final mixture.
एक बर्तन में 80 लीटर दूध है| इसमें से 8 लीटर दूध निकालकर उतना ही पानी मिला दिया जाता है| फिर दूसरी बार 8 लीटर मिश्रण निकालकर उसमे उतना ही पानी मिला दिया जाता है, तो नए मिश्रण में दूध की मात्रा क्या है|
Solution:

Where, c=capacity of vessel
x=Quantity taken out at a time
n=Number of process
Now,
Final quantity=80(1-8/80)²
=80×(9/10)×(9/10)
=64.8 liters Ans.
(Q2)A vessel contains 60 liters of milk. 12 liters of milk is taken out from it and replaced by water. Then again from mixture, 12 liters is again taken out and replaced by water. The ratio of milk and water in the resultant mixture is.
एक बर्तन में 60 लीटर दूध है| इसमें से 12 लीटर दूध निकालकर उतना ही पानी मिला दिया जाता है| फिर दूसरी बार 12 लीटर मिश्रण निकालकर उसमे उतना ही पानी मिला दिया जाता है, तो नए मिश्रण में दूध व पानी का अनुपात है|

Now,
Final quantity=60(1-12/60)²
=60×(4/5)×(4/5)
=38.4 liters
Quantity of water=60-38.4=21.6 liters
∴ Required ratio=38.4 : 21.6
=16:9 Ans.
(Q3)A vessel contains 20 liters of acid. 4 liters of acid is taken out of the vessel and replaced by the same quantity of water. Next 4 liters of the mixture are with drawn, and again the vessel is filled up with water. The ratio of acid left in the vessel with that of the original quantity is.
एक बर्तन में 20 लीटर एसिड है| उसमें से 4 लीटर एसिड निकालकर उसके स्थान पर उतनी ही मात्रा में पानी डाल दिया जाता है| फिर उसमे से 4 लीटर मिश्रण निकाल लिया जाता है और बर्तन में उतनी ही मात्रा में पानी डाल दिया जाता है| बर्तन में बचे एसिड कि मात्रा और प्रारंभ में एसिड की मात्रा का अनुपात क्या होगा|
Solution:

Now,
Final quantity=20(1-4/20)²
=20×(4/5)×(4/5)
=12.8 liters
∴ Required ratio=12.8 : 20
=16:25 Ans.
Ratio And Proportion Problems And Solutions for Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-4.3
(Q1)A container contains two liquids A and B in the ratio 7:5. When 9 liters of mixture are drawn off and the container is filled with B, the ratio of A and B becomes 1:1. How many liters of liquid A was in the container initially?
एक डिब्बे में दो द्रवों A तथा B का मिश्रण 7:5 के अनुपात में है| जब 9 लीटर मिश्रण निकाला गया और डब्बे को B से भर दिया गया, तो A तथा B का अनुपात 1:1 हो गया तो द्रव A की शुरुआती मात्रा कितनी थी|
Solution:

[Concept: जब mixture में से कुछ mixture को यदि निकाला जाए तो निकले गए mixture में भी ratio उतना ही होगा जितना original mixture में था एवं बचे हुए mixture में भी ratio उतना ही होगा जितना original mixture में था| बचे हुए mixture का ratio तब change होगा जब उसमे कुछ extra मिलाया जायेगा|
इस question में बचे हुए mixture में liquid B अलग मिलाया जा रहा है तो liquid B का ratio change होगा but liquid A का ratio उतना ही रहेगा जितना original mixture में था| लकिन question में दिया है कि final ratio 1:1 हो जाता है so final ratio में liquid A के ratio को 7 बनाना होगा ]

2 units=9
1 units=9/2
Initial mixture=12×(9/2)+9
= 63 liters
liquid A=(7/12)×63=36¾ liters Ans.
(Q2)A vessel contains liquid A and B in ratio 5:3. If 16 liters of the mixture are removed and the same quantity of liquid B is added, the ratio becomes 3:5. What quantity does the vessel hold?
एक बर्तन में दो द्रवों A तथा B का मिश्रण 5:3 के अनुपात में है| जब 16 लीटर मिश्रण निकाला गया और डब्बे को द्रव B से भर दिया गया, तो A तथा B का अनुपात 3:5 हो गया तो बर्तन में कुल मात्रा कितनी है|
Solution:


16 unit = 16
1 unit = 16/16=1
Initial mixture=24×1+16
=40 liters Ans.
Second Method:
Quantity of A= (5/8)×16=10
Total quantity=((5+3)² /5² – 3²)×10
=(64/16)×10
= 40 liters Ans.
Note: जब Ratio reverse होगा (i.e 5:3 becomes 3:5) तब हमलोग इस method का use कर सकते है|
(Q3)A can contains a mixture of two liquids A and B in the ratio 7:5. When 9 liters of mixture are drained off and the can is filled with B, the ratio of A and B becomes 7:9. How many liters of liquid A was contained by the can initially?
एक केन में दो द्रवों A तथा B का मिश्रण 7:5 के अनुपात में है| जब 9 लीटर मिश्रण निकाला गया और डब्बे को B से भर दिया गया, तो A तथा B का अनुपात 7:9 हो गया तो द्रव A की शुरुआती मात्रा कितनी थी|

[Concept: इस question में बचे हुए mixture में liquid B अलग मिलाया जा रहा है तो liquid B का ratio change होगा but liquid A का ratio उतना ही रहेगा जितना original mixture में था| so इस question में पहले से ही liquid A same है|]
4 unit = 9
1 unit = 9/4
initial mixture =12×(9/4)+9
=36 liters
liquid A = (7/12)×36
=21 liters Ans.
Ratio And Proportion Examples Shortcut Tricks Type-5
(Q1) The ratio of the income to the expenditure of a family is 10:7. If the family’s expenses are Rs 10,500, then saving of the family is.
एक परिवार की आय और खर्च का अनुपात 10:7 है| यदि परिवार का खर्च Rs 10500 है तो परिवार की बचत ज्ञात करे|
Solution:

Saving = Income – Expenditure
= 10x – 7x = 3x
Given that,
⇒ 7x=10500
⇒ x=1500
∴ saving=3×1500=4500 Ans.
(Q2) The ratio of income and expenditure of a person is 11:10. If he saves Rs 9000 per annum, his monthly income is.
एक व्यक्ति की आय और खर्च का अनुपात 11:10 है| यदि वह RS 9000 हर वर्ष बचत करता है तो मासिक आय ज्ञात करें|
Solution:

Saving = 11x – 10x
= x
Given that,
x = 9000
Annual income=11x=11×9000
=Rs 99000
∴ Monthly income=99000/12=Rs 8250 Ans.
(Q3) The income of A, B and C are in the ratio 7:9:12 and their spendings are in the ratio 8:9:15. If A saves 1/4th of his income, then the saving os A, B and C are in the ratio of.
A, B और C की आय 7:9:12 के अनुपात में है तथा उनके खर्च 8:9:15 के अनुपात में है| यदि A अपनी आय का 1/4 भाग बचाता है, तो A, B और C की बचतों का अनुपात है|
Solution:

56 : 99 : 69 Ans.
[Rough:
According to question
7x-8y = (1/4)×7x
28x-32y=7x
21x=32y
x=32
y=21]
Ratio And Proportion Examples And Solutions For Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-5.1
(Q1)The monthly income of two persons are in the ratio 2:3 and their monthly expenditure are in the ratio 5:9. if each of them saves Rs 600 per month, then their monthly incomes are.
दो व्यक्तियो की मासिक आय 2:3 के अनुपात में है तथा उनका मासिक व्यय 5:9 के अनुपात में है| यदि इनमें से प्रत्येक प्रतिमास Rs 600 की बचत करता है, तो उनकी मासिक आय है|
Solution:
Let the income of 1st and 2nd person are 2x and 3x
[Note: Income(I)=Expenditure(E) + Saving(S)]
∴ I – S = E
Now according to the question

⇒ 18x – 5400 = 15x – 3000
⇒ 3x = 2400
∴ x=800
Income of 1st person=2x=2×800
=Rs 1600 Ans.
Income of 2nd person=3x=3×800
=Rs 2400 Ans.
Second Method:
Step-1: सबसे पहले Income और Expenditure को cross-multiply करना है फिर उसके बाद difference निकालना है|

Step-2: Expenditure और Saving को cross-multiply करना है फिर उसके बाद difference निकालना है|

3 unit = 2400
1 unit = 800
Income of 1st person=2unit=Rs 1600 Ans.
Income of 2nd person=3unit=Rs 2400 Ans.
(Q2)The incomes of two persons are in the ratio 3:2 and their expenditure are in the ratio 5:3. If each saves Rs. 1000, then 1st person income is.
दो व्यक्तियो की मासिक आय 3:2 के अनुपात में है और उनका खर्च 5:3 के अनुपात में है| यदि प्रत्येक Rs 1000 बचाता है, तो पहले व्यक्ति की आय कितनी है|
Solution:
Let the income of 1st and 2nd person are 3x and 2x
[Note: Income(I)=Expenditure(E) + Saving(S)]
∴ I – S = E
Now according to the question

⇒ 9x – 3000 = 10x – 5000
⇒ x = 2000
Income of 1st person=3x=3×2000
=Rs 6000 Ans.
Second Method
Step-1: सबसे पहले Income और Expenditure को cross-multiply करना है फिर उसके बाद difference निकालना है|

Step-2: Expenditure और Saving को cross-multiply करना है फिर उसके बाद difference निकालना है|

1 unit = 2000
Income of 1st person=3unit
=Rs 6000 Ans.
Ratio And Proportion Examples And Solutions For Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-5.2
(Q1) The ratio of income of two persons is 5:3 and that of their expenditures is 9:5. Find the income of each person, if they save Rs 1300 and Rs 900 respectively.
दो व्यक्तियो की आय का अनुपात 5:3 है तथा उनके व्यय का अनुपात 9:5 है| यदि ये क्रमशः Rs 1300 और Rs 900 की बचत करते हैं, तो प्रत्येक की आय ज्ञात कीजिए|
Solution:
Let the income of 1st and 2nd person are 5x and 3x
Note: Income(I)=Expenditure(E) + Saving(S)
I – S = E
Now according to the question

⇒ 25x – 6500 = 27x – 8100
⇒ x= 800
Income of 1st person=5x=5×800
=Rs 4000 Ans.
Income of 2nd person=3x=3×800
=Rs 2400 Ans.
Second Method
Step-1: सबसे पहले Income और Expenditure को cross-multiply करना है फिर उसके बाद difference निकालना है

Step-2: Expenditure और Saving को cross-multiply करना है फिर उसके बाद difference निकालना है|

2 unit = 1600
1 unit = 800
Income of 1st person=5unit=Rs 4000 Ans.
Income of 2nd person=3unit=Rs 2400 Ans.
(Q2) Two person have their monthly incomes in the ratio 8:5, while their monthly expenditures are in the ratio 5:3. If they have saved Rs 12000 and Rs 10000 monthly respectively, then the difference in their monthly income is.
दो व्यक्तियो की मासिक आय 8:5 के अनुपात में है जबकि उनका मासिक व्यय 5:3 के अनुपात में है| यदि उन्होंने क्रमशः Rs 12000 और Rs 10,000 की मासिक बचत की हो, तो उनकी मासिक आय में अंतर कितना है|
Solution:
Let the income of 1st and 2nd person are 5x and 3x
[Note: Income(I)=Expenditure(E) + Saving(S)]
∴ I – S = E
Now according to the question

⇒ 24x-36000=25x-50000
⇒ x=14000
Income of 1st person=8x=8×14000
=Rs 112000
Income of 2nd person=5x=5×14000
=Rs 70000
Difference=112000-70000=42000 Ans.
OR
Difference in monthly income=8x-5x=3x
=3×14000=42000 Ans.
Second Method
Step-1: सबसे पहले Income और Expenditure को cross-multiply करना है फिर उसके बाद difference निकालना है

Step-2: Expenditure और Saving को cross-multiply करना है फिर उसके बाद difference निकालना है|

Difference in monthly income=8-5=3
Now,
1 unit=14000
3 unit=14000×3=42000 Ans.
Ratio And Proportion Examples And Solutions For Bank PO, SSC CGL, SSC CHSL, Railway, Lic Exam Type-5.3
(Q1) A box contains 280 coins of one-rupee, 50-paise and 25-paise. The values of each kind of the coins are in the ratio of 8:4:3. Then the number of 50-paise coins is.
एक बॉक्स में Rs 1, 50 पैसे और 25 पैसे के 280 सिक्के है| प्रत्येक प्रकार के सिक्के के मूल्य 8:4:3 के अनुपात में हैं, तो 50 पैसे के सिक्कों की संख्या बताइए|
Solution:
[Concept: 50 पैसे को Rs 1 बनाना है तो 50 पैसे को 2 से multiply करना होगा या यह भी कह सकते है 50 पैसे के 2 सिक्के लेंगे| इस प्रकार 50 पैसे के total 8 सिक्के होंगे(i.e 4×2=8)| 25 पैसे को Rs 1 बनाना है तो 25 पैसे को 4 से multiply करना होगा या यह भी कह सकते है 25 पैसे के 4 सिक्के लेंगे| इस प्रकार 25 पैसे के total 12 सिक्के होंगे(i.e 3×4=12)|]

Total no of coins=28
28 coins =280
1 coins = 10
No. of 50 paise coins = 8×10 =80 Ans.
(Q2) There are 480 coins in half rupees, quarter rupees and 10 paise coins and their values are proportional to 5:3:1. The number of coins in each case are.
50 पैसे, 25 पैसे और 10 पैसे के कुल 480 सिक्के है| उनका मूल्य 5:3:1 के अनुपात में है तो प्रत्येक सिक्कों की संख्या कितनी है|
Solution:
[Concept: 50 पैसे को Rs 1 बनाना है तो 50 पैसे को 2 से multiply करना होगा या यह भी कह सकते है 50 पैसे के 2 सिक्के लेंगे तो इस प्रकार 50 पैसे के total 10 सिक्के होंगे(i.e 5×2=10)| 25 पैसे को Rs 1 बनाना है तो 25 पैसे को 4 से multiply करना होगा या यह भी कह सकते है 25 पैसे के 4 सिक्के लेंगे तो इस प्रकार 25 पैसे के total 12 सिक्के होंगे(i.e 3×4=12)| 10 पैसे को Rs 1 बनाना है तो 10 पैसे को 10 से multiply करना होगा या यह भी कह सकते है 10 पैसे के 10 सिक्के लेंगे तो इस प्रकार 10 पैसे के total 10 सिक्के होंगे(i.e 1×10=10)|]

Total no of coins=32
32 coins =480
1 coins = 15
No. of 50 paise coins = 10×15 =150 Ans.
No. of 25 paise coins = 12×15 =180 Ans.
No. of 10 paise coins = 10×15 =150 Ans.
Theory: When the ratio between first and second given numbers/quantities is P: and the ratio between second and third given numbers and quantities is R : S, then the ratio of all the three given numbers/quantities will be –
Let’s take a look at some examples for this quant shortcut trick
Example 1 : If X : Y = 3 : 4 and Y : Z = 3 : 2 Then , X : Y : Z = ?
(1) 6 : 12 : 8
(2) 9 : 12 : 8
(3) 3 : 6 : 4
(4) 12 : 9 : 8
(5) 9 : 8 : 12
Solving this by our shortcut:
X : Y : Z = 3 × 3 : 4 × 3 : 4 × 2
= 9 : 12 : 8
Hence, Choice 5 is correct
Example 2: If P : Q = 5 : 7 and Q : R = 4 : 9 Then , P : Q : R = ?
(1) 20 : 63 : 28
(2) 63 : 28 : 20
(3) 20 : 28 : 63
(4) 45 : 28 : 63
(5) None of these.
Solving this by our shortcut:
P : Q : R = 5 × 4 : 7 × 4 : 7 × 9
= 20 : 28 : 63
Hence, Choice 4 is correct
Example 3. When the ratio between the first and the second given numbers /quantities is 3 : 4 and the ratio between the second and the third given numbers /quantities is 2 : 3 and the sum of all these three numbers/quantities is 104. Then find out the third number.
(1) 12
(2) 24
(3) 36
(4) 48
(5) None of these.










