Trigonometry Tricks – 4 [Maximum and Minimum Values]

Few points to remember:

1. sinθ and cosθ both have “1” as their maximum value and “-1” as their minimum value. Hence the values of sinx, sin2x, cosx, cos3x, etc. lie between -1 and 1.
2. For sin²x and cos²x
   • Minimum value = 0
   • Maximum value = 1
3. For sinxcosx
   • Minimum value = -1/2
   • Maximum value = 1/2
4. Minimum value of (sin θ cos θ)n = (-1/2)n
5. 

Some SSC CGL questions :

1. 1) What is the least value of 2sin²θ + 3cos²θ

       (A) 1            (B) 2             (C) 3            (D) 0

Since 2 is less than 3
Minimum value = 2

      Answer: (B)

     Hence the least value of 4sec²θ + 9cosec²θ = 13 + 12 = 25

 Answer: (C)

1. 4) The maximum of 3sinx – 4cosx is

       (A) -1               (B) 5                (C) 7               (D) 9

Maximum value = √(3^2 + 4^2) = √25 = 5
Answer: (B)

Sometimes they ask the minimum/maximum value of a function. In CGL, that function would always be quadratic (ax² + bx + c). Please note that a quadratic function can’t have both maximum and minimum values. 

• If “a” is positive, then the quadratic function will only have a minimum value. The maximum value would be infinite.
• If “a” is negative, then the quadratic function will only have a maximum value. The minimum value would be infinite.

But the process to find both minimum and maximum values is same. Hence you shouldn’t be worried about the words “maximum” or “minimum”. When finding the minimum/maximum value of a function, we use the concept of “differentiation”. Although differentiation is a wide topic in itself, but for CGL purpose, we only have to learn the basics.

Just remember following things:

1. Differentiation of axⁿ = a*n*x^n-1. Hence differentiation of 4x³ = 12x² and differentiation of 3x² = 6x
2. Differentiation of ax = a. Hence differentiation of 4x is 4.
3. Differentiation of any constant is zero. Hence differentiation of 5 is 0.
4. If you have to differentiate ax² + bx + c, just differentiate each of its term separately and add the result.
5. Process of finding the minimum value of a function :
   1. Differentiate the function
   2. What ever result you get, equate it with zero
   3. Find the value of x
   4. Put this value of x in the original function to get the minimum value.

Let us solve a CGL question:
Q. 5) Find the minimum value of (x – 2)(x – 9)
(A) -11/4             (B) 49/4             (C) 0            (D) -49/4 

(x – 2)(x – 9) = x^2 – 11x + 18

Now we will differentiate (x^2 – 11x + 18)

Note that in this question, the value of a is positive, i.e., +1 and hence the question has asked you the “minimum” value. Had the value of “a” been negative (like -1), they would have asked you the “maximum” value.

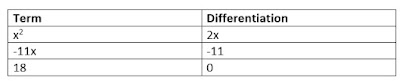
Hence, differentiation of (x^2 – 11x + 18) = 2x – 11

Now 2x – 11 = 0

x = 11/2

Put x = 11/2 in (x^2 – 11x + 18) to get the minimum value

Minimum value of x^2 – 11x + 18 = (11/2)^2 – 11*(11/2) + 18 = -49/4

Answer: (D)

If you have any doubt in this article, please drop a comment…
Keep reading 🙂