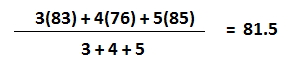Mixtures & Alligations Tricks & Tips
Mixture & Alligation Short-Cut Tricks & Tips : Fillers Short-Cut Tricks & Tips Question Pdf for Banking, SSC, RRB, FCI, Railway, UPSC, State PCS, Insurance & other Competitive exams. Mixture & Alligation Short-Cut Tricks & Tips shortcut Tricks Pdf, Mixture & Alligation Short-Cut Tricks & Tips MCQ, Mixture & Alligation Short-Cut Tricks & Tips Objective Question & Answer Pdf. “Fillers Short-Cut Tricks & Tips Questions PDF” In this post we are providing you the Mixture & Alligation Short-Cut Tricks & Tips pdf with detailed solution & Short Tricks. So that you can easily get the logic of question. This Mixture & Alligation Short-Cut Tricks & Tips Pdf we are Providing is free to download. ” Most Important Fillers Short-Cut Tricks & Tips Question PDF with Answers“
Mixture & Alligation Short-Cut Tricks & Tips Plays a vital role in Exam. In every exam you will get at least 5-10 questions from this topic. So candidates must focus on this topic and download this Mixture & Alligation Short-Cut Tricks & Tips pdf to get important questions with best solution regarding Mixture & Alligation Short-Cut Tricks & Tips. We have put all Previous Year Questions of Mixture & Alligation Short-Cut Tricks & Tips that are Asked in various Govt & Private Exam.
INTRODUCTION TO MIXTURE AND ALLIGATION:
Hi Aspirants today we are going to discuss on a topic Mixture and Alligation. This topic carries 1 mark in prelims and 2 mark in mains exam.This topic can be implemented in Topics such as Time and Distance ,Ratio and Proportions.
MIXTURE:
When two or more components are mixed together then it is known as Mixture
Mixture is of two types they are:
1.Simple Mixture:When two or more different ingredients are mixed together,a simple mixture is formed
2.Compound Mixture:When two or more simple mixtures are mixed together, a compound mixture is formed.
ALLIGATION:
It enables us to find the ratio in which two or more ingredients at the given price must be mixed to produce a mixture of desired price.
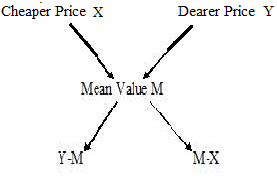
Where M=Mean Value which is between X and Y, X=Cheaper Price, Y=Price higher than the Mean Value
#.1.TYPE 1:
MIXTURE CONTAINING TWO OR MORE INGREDIENTS:
1.A Shopkeeper Sells Rice Of 1kg For Rs.75 W Two Quality Of Rice Whose Worth For 1kg Is Rs.70 And Rs.80.
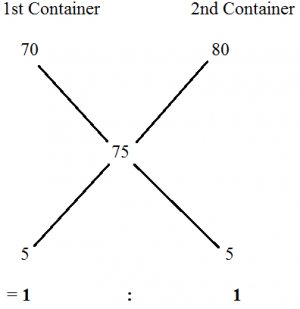
Therefore for 1kg of rice the two quality of rice should be mixed in the ratio 1:1
TYPE 2:
BASED ON PROFIT OR LOSS:
1.A Dishonest Milkman Professes To Sell His Milk At Cost Price But He Mixes It With Water And Thereby Gains 25%.The Percentage Of Water In The Mixture?
Let the Cost Price of Pure Milk be Rs.1,
Selling Price of (Milk+ Water) is also Rs.1. which is 25% more than the Costprice
Therefore CostPrice = (100/125)*1=(4/5)
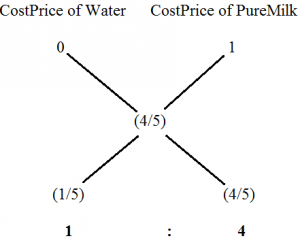
The Percentage of water mixed in the mixture =*100=20%
2.The Ratio ,In Which Tea Costing Rs.192 Per Kg Is To Be Mixed With Tea Costing Rs.150 Per Kg So That The Mixed Tea When Sold For Rs.194.40 Per Kg,Gives A Profit Of 20%.
| Quality | Cost Price | Selling Price | Selling Price after Profit/Loss |
| 1st Quality | 150 | 194.40 after 20% profit | |
| 2nd Quality | 192 |
Finding Selling Price after Giving Profit over Cost Price:
Let the Cost Price be X
Selling Price=X*(120/100) = 194.40
X=(19440/120) ⇒ X=162
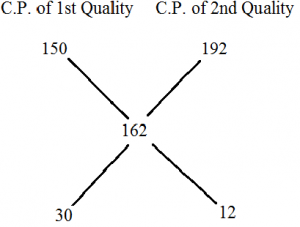
30:12 ⇒ 5:2
The 1st and 2nd quality of rice should be mixed in the ratio:5:2
Remember:
If there is a loss in the transaction indicate it by the ‘-‘ negative sign before the number.
TYPE 1:
BASED ON THREE INGREDIENTS OR THREE RATIO’S:
1.The Grocer sells apples of 3 varieties whose price per kg’s are Rs.40,Rs.60 and Rs. 90 .If he sells 1kg of apple by missing all these 3 varieties for Rs.80 what is the ratio by which these varieties are to be mixed?
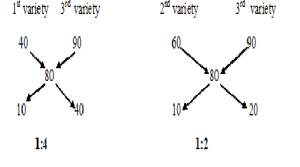
| 1st variety | 3rd variety | 2nd variety
|
| 1 | 4 | |
| 2 | 1 |
Ratio’s by which these 3 Qualities are missed are=1:2:4
2.Tea worth Rs.126 per kg and Rs.135 per kg are mixed with a third variety in the ratio 1:1:2.If the mixture is worth Rs.153 per kg, the price of the third variety per kg will be?
Given that the tea worth Rs.126 and Rs.135 per kg is mixed in the ratio 1:1.
Therefore price for 1kg= = Rs.130.50
Now we have two price 130.50 and the price of the third variety is X
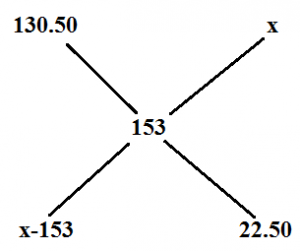
The price of the third variety=Rs.175.50
3.There are three vessels of equal capacity holds milk and water in the ratio of 1:2,2:3 and 1:4if the content of all the three vessel s are mixed in asingle vessel then.Find the ratio of milk and water in the new vessel?
Here there are three ratio’s
1:2=3Part
2:3=5Part
1:4=5Part
Lcm =15Litres
| Milk | Water |
| 5Litres | 10Litre |
| 6Litre | 9Litre |
| 3Litre | 12Litre |
| 14Litres | 31Litre |
The new Ratio is 14:31
TYPE 2:
BASED ON REMOVING AND ADDING SOME QUANTITY :
1)How much water must be added to 60 litres of milk at 1.5 litre for Rs.20,So as to have a mixture worth Rs.10 2/3 per litre?
C.P for 1.5 litre of milk =Rs.20
C.P for 1 litre of milk=Rs.40/3
C.P for 1 litre of water=Rs.0
Given Mean value=Rs.32/3
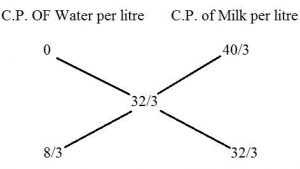
8/3 : 32/3= 1:4
Therefore water in the mixture in 60 litres is (1/5)*60=12 litres
2)In a 729 litres mixture of milk and water ,the ratio of milk to water is 7:2.To get a new mixture containing milk and water in the ratio 7:3,the amount of water to be added is?
| 729 | |
| 7x | 2x |
9x=729 x=81
Old Mixture New Mixture
7:2 7:3
Already the mixture contains water in the proportion 2x and the new mixture contains water in the proportion 3x .So x quantity of water is added to the mixture .Therefore 81 litres of water is added to the new mixture.
3)8 litres are drawn from a cask filled with wine and is then filled with water .This operation is performed three more times.The ratio of the quantity of wine now left in the cask to that of the total solution is 16:81.How much wine does the cask originally ?
When the final amount of solute that is not replaced calculated as:
Initial Amount * (Volume After Removal/Volume After Replacing)^n
Final ratio of solute not replaced to total is
Initial Ratio * (Volume After Removal/Volume After Replacing)^n
Here let us assume the initial value is 1 then Wine .Let the Quantity of wine in the cask originally be x
Therefore
1* [(x-8)^4/x]
=[16/81]
x=24litres
Wine originally in the cask is 24 Litres
4)A vessel contains mixture of liquids A and B in the ratio 3:2.When 20 litres of the mixture is taken out and replaced by 20litres of liquid B,the ratio changes to 1:4.How many litres of liquid A was there initially present in the vessel?
Original ratio=3:2
3/5 * (5X-20)/5x=1/4
X=6 then the liquid A in the vessel =3X=3*6=18Litres
IMPORTANCE OF MIXTURE AND ALLIGATION:
Mixture and Alligation is used in other Miscellaneous Topic such as
Ratio and Proportion
Time and Distance
You can reduce the time taken to solve the problem if you use Mixture and Alligation Method
#.1.TYPE 1:
BASED ON ALLOYS:
1.A milk vendor has 2 cans of milk. The first contains 25% water and he rest milk.The second container 50% water.How much milk should he mix from each of the containers so as to get 12 litres of milk such that the ratio of water to milk is 3:5?
Given that
Milk in 1st Can = 3/4
Milk in 2nd Can =1/2
We want milk in the ratio=5/8
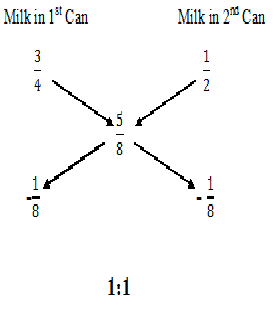
(1/2)*12=6litres So, quantity of mixture taken from each can=6litre
2.The milk and water in two vessels A and B are in the ratio 4:3 and 2:3 respectively .In what ratio the liquids in both vessels be mixed to obtain a new mixture in vessel c consisting half milk and half water?
Mean Value=(1/2)
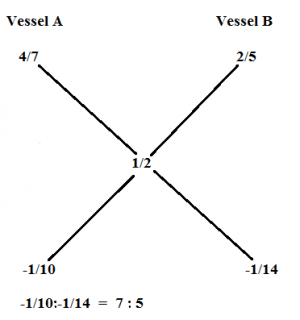
Therefore Milk and Water should be mixed in the Ratio of 7:5
#.2 TYPE 2:
FINDING NUMBER OF PERSONS :
1.In a zoo there are Rabbits and Pigeons.If heads are counted ,there are 200 and if legs are counted there are 580.How many pigeons are there?
Total heads Count=200
Total Legs Count=580
Average Leg Count =580/200
= 29/10
Average leg Count for Rabbit =4,
Average leg Count for Pigeons=2
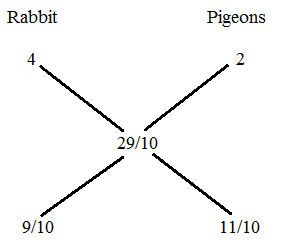
9:11
Thus the number of Pigeons is * 200=110 pigeons
2.The total number of people in the village is 5000.If the male and female increases by 10% and 15% respectively,the population of the village becomes 5600.What is the number of male in the village?
Total number of people in the village=5000
10% of the village =500 15% of the village=750
Increased number of people=5600-5000=600
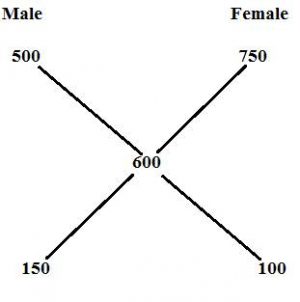
=150:100
=3:2
Male in village=3000 ⇒ (5000*3/5=3000)
#.3. TYPE 3:
PARTIAL WORK:
1.A shopkeeper sells 1000kg of sugar ,part of which he sells at 8% profit and the rest at 18% profit .He gains 14% on the whole. The quantity sold at Rs.18% is?
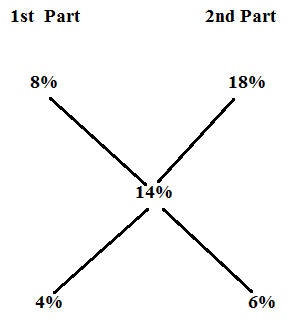
4:6
=2:3
Therefore the 1000kg sugar is sold in the ratio 400:600
Sugar sold at the profit of 18%=600kg
1)BASED ON FINDING INDIVIDUAL CAPACITY
2)BASED ON DIFFERENT CAPACITY
3)BASED ON RATIO’S
1)A Jar Contains A Mixture Of Milk & Water In The Ratio 4:1.When 10 Litres Of The Mixture Is Taken Out & 10 Litres Of Water Is Poured Into The Jar,The Ratio Becomes 2:3.How Many Litres Of Milk Was In The Jar?

PRACTICE THIS SUM:
1)A Vessel Contains mixture of liquids A and B in the ratio 3:2.When 20 litres of the mixture is taen out and replaced by 20 litres of liquid B,the ratio changes to 1:4.How many litres of liquid A was there initially present in the vessel?
2)A can contains a mixture of two liquids in proportion 7:5.When 9 litres of mixture are drawn off and the can is filled with B,the proportion of A and B becomes 7:9.How many litres of liquid A was contained by the can initially?
#.2.TYPE 2:
BASED ON DIFFERENT CAPACITY:
1)Three glasses of Sizes 5 litres,10 litres & 15 litres contain mixture of Milk & Water in the ratio 3:2,4:6&4:11 respectively.The Contents of all the three glasses are poured into single vessel.Find the ratio of Milk to Water in the resultant mixture.
To find the Ratio of Milk to Water in the resultant Mixture,


PRACTICE THIS SUM:
1)Three bottle of Capacity 6 Litres,12 Litres and 4 litres contain mixture of Sugar water and honey in the ratio 1:5 , 7:5 & 1:3 respectively.The contents of all the three bottles are poured into single bottle.Find the ratio of Sugar water to honey in the resultant mixture?
2)Four glasses of sizes 2Litres,8 Litres,12 Litres & 16 Litres contain mixture of milk & Water in the ratio 1:1 ,3:5,7:5,9:7 respectively.The Contents of all the four glasses are poured into single glass.Find the ratio of Milk & Water in the resultant Mixture?
#.3. TYPE 3:
BASED ON RATIO’S:
1)In an Alloy,Zinc and Copper are in the ratio 3:4,In the Second alloy the same elements are mixed in the ratio 7:2.In what ratio should these two alloys be mixed to form a new alloy in which the two elements are in the ratio 5:6?
The ratio is written as
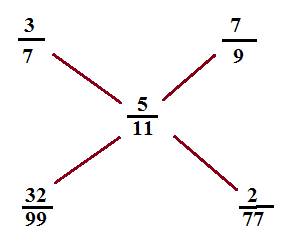
The ratio is 32/99:2/77
PRACTICE THIS SUM:
1)In An Alloy The Zinc & Copper Are In The Ratio 1:3.In The Second Alloy The Same Elements Are In The Ratio 4:3.In What Ratio Should These Two Alloys Be Mixed To Form A New Alloy In Which The Two Elements Are In The Ratio 4:5?
2)A jar full of lime juice contains juice and sugar water in the ratio 2:3.In the 2nd Jar the same elements are in the ratio 7:2.In what ratio should these two elements be mixed to for a new alloy in which the two elements are in the ratio 6:5?
“One Topic, to rule them all”
Alligation is a method of solving arithmetic problems related to mixtures of ingredients. Please note that alligation method is applied for percentage value, ratio, rate, prices, speed, etc. and not for absolute value. That is whenever per cent, per km, per hour, per kg, are being compared, we can use Alligation.
Common trick for Ratio-Proportion and Mixture Alligation : Almost 50% of the questions are solvable just by going through the options. Just go through the questions I have solved in this article and you will know the approach.
Rule of Alligation
if the gradients are mixed in a ratio, then
![]()
We represent it as under:

Then, (cheaper quantity) : (dearer quantity) = (d – m ) : (m – c)
Q.1
Given SP = Rs. 320/kg, Profit = 20%
Hence CP = 320/1.2 = Rs. 800/3
So the Mean price is Rs. 800/3 per kg
Now you can apply the formula-
Type 1 : Type 2 = 280 – 800/3 : 800/3 – 180 = 2 : 13
Answer : (B)
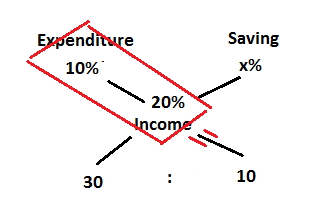
Both the containers have equal capacity. Let us assume that both containers are of 28 litres. Why 28? Because 28 is the LCM of (3 + 1) and (5 + 2) or 4 and 7. So taking the capacity as 28 litres will make your calculations easier.
In Container 1, we have (3/4)*28 = 21 litres of milk and (1/4)*28 = 7 litres of water.
In Container 1, we have (5/7)*28 = 20 litres of milk and (2/7)*28 = 8 litres of water.
Total milk in both the containers = 21 + 20 = 41
Total water in both the containers = 7 + 8 = 15
Milk : Water = 41 : 15
Answer : (D)
Shortcut
Container 1 has 3 times more milk than water
Container 2 has 2.5 times more milk than water
When the contents of the two containers are mixed, the milk will still be more than water. How much more ? Somewhere between 2.5 and 3 times
(D) is the only option where the quantity of milk is around 2.7 times (i.e. between 2.5 and 3) that of the water.
Milk in vessel A = 4/7
Milk in vessel B = 2/5
Milk in vessel C = 1/2 (because in vessel C, milk and water are present in 1:1 ratio)
You have to mix 4/7 and 2/5, to produce 1/2. Hence 1/2 is the Mean Price.
A : B = (1/2 – 2/5)/(4/7 – 1/2) = 14 : 10 = 7 : 5
Shortcut
Final ratio of the three varieties is 5 : 7 : 9
The question asks us the quantity of third variety of tea in the final mixture. From the above ratio, it is clear that the quantity of the third variety is a multiple of 9. So 45 is the only option possible.
Answer : (D)
Method
Let the three quantities be 4x, 5x and 8x
New quantities are 4x + 5, 5x + 10 and 8x + p
Now 4x + 5 : 5x + 10 : 8x + p = 5 : 7 : 9
(4x + 5)/(5x + 10) = 5/7 and (4x + 5)/(8x + p) = 5/9
Solving 1st equation, we get x = 5
Solving 2nd equation, we get p = 5
In the final mixture the quantity of the third variety is 8x + p = 8*5 + 5 = 45
In this question we will use the below formula
So from the above formula
(Quantity of acid left)/(Quantity of acid in the original mixture) = (1 – 4/20)^2 = 16:25
Answer : (A)
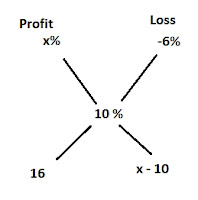
Let the original quantities of A and B be 4x and x
In 10 litres, quantity of A = 4/5 * 10 = 8 litres
In 10 litres, quantity of B = (10 – 8) = 2 litres
New quantities of A and B are 2x and 3x
(Original Quantity of A) – (New quantity of A) = 8 litres[Because after taking out 10 litres of the mixture, the quantity of liquid A reduced by 8 litres]
So, 4x – 2x = 8
or x = 4
Hence quantity of liquid A in original mixture = 4*4 = 16 litres
Answer : (C)
Note : In the above question, there were two different ratios 4:1 and 2:3, then too I took the same constant of proportionality for them, i.e. ‘x’ because the following two conditions were met:
1. The volume of mixture did not change (Like in this question 10 litres were replaced, not removed)
2. The two ratios had same no. of parts (4:1 and 2:3 both have 5 parts)
You can take different constant to solve the question, but that will make the calculations little lengthy.
Since the ratio of alcohol and water is 1:4, hence quantities of alcohol and water in the mixture are 3 litres and 12 litres respectively.
Total volume will become 18 litres after adding 3 litres water
% of alcohol = 3/18 * 100 = 50/3%
Answer : (B)
Q. 8)
Let us solve some CGL questions that may not seem to belong to Mixture-Alligation category, but are easier to solve via Alligation formula…
Alternate method
This method is equally easy.
Let the distance travelled on foot be X km. Then distance travelled on bicycle = (61 – X)
Now he travelled for 9 hours. Hence
X/4 + (61 – X)/9 = 9
Solve for X
You will get X = 16 km
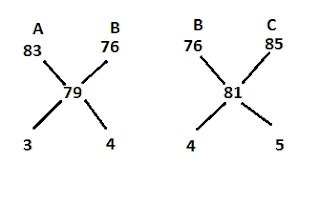
A : B = 3 : 4 and B: C = 4 : 5
A : B : C = 3 : 4 : 5
Average score of classes A, B and C =
Practice Sets On Mixtures & Alligations
- An alloy contains iron, copper and zinc in the ratio of 3:4:2. Another alloy contains copper, zinc and tin in the ratio of 10:5:3. If equal quantities of both alloys are melted, then weight of tin per kg in the new alloy
a) 1/8 kg
b) 1/10 kg
c) 1/12 kg
d) 1/14 kg
e) None of these - 8 litres are drawn from a flask containing milk and then filled with water. The operation is performed 3 more times. The ratio of the quantity of milk left and total solution is 81/625. How much milk the flask initially holds?
a) 10ltr
b) 20ltr
c) 30ltr
d) 40ltr
e) None of these - A 40 litre mixture contains milk and water in the ratio of 3:2. 20 litres of the mixture is drawn of and filled with pure milk. This operation is repeated one more time. At the end what is the ratio of milk and water in the resulting mixture?
a) 5:1
b) 6:1
c) 8:1
d) 9:1
e) None of these - Two vessels contain milk and water in the ratio of 7:3 and 2:3 respectively. Find the ratio in which the contents of both the vessels must be mixed to get a new mixture containing milk and water in the ratio 3:2.
a) 2:1
b) 2:3
c) 3:1
d) 3:5
e) None of these - How many Kgs of rice A costing rupees 20 per kg must be mixed with 20 kg of rice B costing rupees 32 per kg, so that after selling them at 35 rupees per kg, he gets a profit of 25%.
a) 10 kg
b) 40 kg
c) 24 kg
d) 25 kg
e) None of these - How many litres of water must be added to 60 litre mixture that contains milk and water in the 7:3 such that the resulting mixture has 50% water in it?
a) 12
b) 16
c) 24
d) 28
e) None of these - A sample of x litre is replaced from a container containing milk and water in the ratio 2:3 by pure milk. If the container hold 30 litres of the mixture, and after the operation proportion of milk and water is same. Find the value of X?
a) 4
b) 5
c) 6
d) 7
e) None of these - Two cans P and Q contains milk and water in the ratio of 3:2 and 7:3 respectively. The ratio in which these two cans be mixed so as to get a new mixture containing milk and water in the ratio 7:4.
a) 4:7
b) 7:3
c) 7:4
d) 7:5
e) None of these - A trader mixes 6ltr of milk costing 5000 rupees with 7ltr of milk costing 6000 rupees per litre. The trader also mixes some quantity of water to the mixture so as to bring the price to 4800 per litre. How many litres of water is added
a) 1ltr
b) 2ltr
c) 3ltr
d) 4ltr
e) None of these - How many kilograms of rice costing Rs. 9 per kg must be mixed with 27kg of rice costing Rs.7 per kg so that there may be gain of 10% by selling the mixture at Rs.9.24 per kg?
a) 63
b) 56
c) 49
d) 35
e) None of these
- A man buys milk at the rate of 5 rupees per litre and mixes it with water. By selling the mixture at Rs 4 a litre he gains 25 percent. How much water did each litre of the mixture contain?
a) 9/25
b) 11/25
c) 16/25
d) 19/25
e) None of these - A mixture containing milk and water in the ratio 3:2 and another mixture contains them in the ratio 4:5. How many litres of the later must be mixed with 3 litres of the former so that the resulting mixture may contain equal quantities of milk and water?
a) 3.3/4 litre
b) 4.1/2 litre
c) 5.2/3 litre
d) 5.2/5 litre
e) None of these - Two vessels contain milk and water in the ratio of 7:3 and 2:3 respectively. Find the ratio in which the contents of both the vessels must be mixed to get a new mixture containing milk and water in the ratio 3:2.
a) 2:1
b) 2:3
c) 3:1
d) 3:5
e) None of these - In 80 litre mixture of milk and water, water content is 40 percent. The trader gives 20 litre of the mixture to the customer and adds 20 litres of water to the mixture. What is the final ratio of milk and water in the mixture?
a) 9:13
b) 9:11
c) 11:9
d) 12:7
e) None of these - 70 litres of a mixture of milk and water contains 20% water. How much water should be added so that the mixture has 28% water?
a) 50/9 litre
b) 60/9 litre
c) 70/9 litre
d) 100/9 litre
e) None of these - Rice worth Rs. 110 per kg and Rs. 95 per kg are mixed with a third variety in the ratio 1:1:2. If the mixture is worth Rs. 115 per kg, the price of the third variety per kg will be
a) 117.5
b) 127.5
c) 137.5
d) 147.5
e) None of these - A trader has 60 kg of pulses, one part of which is sold at 8% profit and the rest is sold at 14% profit. He gains 12% on whole. What is the quantity sold at 14% profit?
a) 20kg
b) 30kg
c) 40kg
d) 50kg
e) None of these - Two cans of 60 and 80 litres are filled with the mixtures of milk and water. The proportion of milk and water in the cans being 5:7 and 9:7 respectively. If the contents of the two cans are mixed and 30 litres of the water is added to the whole, then find the ratio of milk and water in the final mixture?
a) 7:9
b) 7:10
c) 8:11
d) 9:7
e) None of these - There are three vessels each of 20 litre capacity is filled with the mixture of milk and water. The ratio of milk and water are 2:3, 3:4 and 4:5 respectively. All the vessels are emptied into fourth vessel, then find the ratio of milk and water in the final mixture.
a) 401/543
b) 401/544
c) 401/545
d) 401/546
e) None of these - In two alloys copper and zinc are in the ratio of 1:4 and 3:1 respectively. 20 kg of first alloy and 32 kg of second alloy and some pure zinc are melted together. An alloy is obtained in which the ratio of copper and zinc was 3:5. Find the quantity of zinc melted.
a) 65/3 kg
b) 67/3 kg
c) 68/3 kg
d) 71/3 kg
e) None of these - In two alloys copper and zinc are in the ratio of 1:3 and 4:1 respectively. 20 kg of first alloy and 35 kg of second alloy and some quantity of pure zinc is melted together. The final alloy has copper and zinc in the ratio of 5:4. Find the amount of pure zinc melted.
a) 4.2
b) 4.4
c) 4.6
d) 4.8
e) None of these - In what ratio three kinds of rice costing 1.45rs, 1.54rs and 1.70rs must be mixed so that the mixture can be sold at 1.65rs per kg.
a) 11:21:44
b) 20:11:44
c) 11:20:44
d) 44:20:11
e) None of these - A container filled with liquid containing 4 parts of water and 6 parts of milk. How much of mixture must be drawn off and filled with water so that the mixture contains half milk and half water.
a) 1/4
b) 1/3
c) 1/6
d) 1/5
e) None of these - A trader has 1500 kg of wheat. One part of it is sold at 10 percent profit and other part at 18 percent profit. He gains a total of 16 percent on the whole lot. The quantity sold at 10% is-
a) 275
b) 375
c) 475
d) 575
e) None of these - Two cans P and Q contains milk and water in the ratio of 3:2 and 7:3 respectively. The ratio in which these two cans be mixed so as to get a new mixture containing milk and water in the ratio 7:4.
a) 4:7
b) 7:3
c) 7:4
d) 7:5
e) None of these - A dishonest seller professes to sell his milk at cost price but he mixes water with milk and gains 25 percent, then find the percentage of milk in the mixture.
a) 60%
b) 70%
c) 80%
d) 90%
e) None of these - Fresh fruit contains 75 percent water and dry fruit contains 20 percent water. How much dry fruit can be obtained from 150 kg of fresh fruit.
a) 45
b) 46
c) 47
d) 48
e) None of these - How much water must be added to 50 litre of milk costing 10 rupees per litre so as to bring the cost of milk to 8 rupees per litre.
a) 11.5
b) 12.5
c) 13.5
d) 14.5
e) None of these - A trader mixes 6ltr of milk costing 5000 rupees with 7ltr of milk costing 6000 rupees per litre. The trader also mixes some quantity of water to the mixture so as to bring the price to 4800 per litre. How many litres of water is added
a) 1ltr
b) 2ltr
c) 3ltr
d) 4ltr
e) None of these - There are three vessels each of 20 litre capacity is filled with the mixture of milk and water. The ratio of milk and water are 2:3, 3:4 and 4:5 respectively. All the vessels are emptied into fourth vessel, then find the ratio of milk and water in the final mixture.
a) 401/543
b) 401/544
c) 401/545
d) 401/546
e) None of these