Pie Chart DI Tricks & Tips
Pie Chart DI Data Interpretation Short-Cut Tricks & Tips : Pie Chart DI Data Interpretation Short-Cut Tricks & Tips Question Pdf for Banking, SSC, RRB, FCI, Railway, UPSC, State PCS, Insurance & other Competitive exams. Pie Chart DI Data Interpretation Short-Cut Tricks & Tips shortcut Tricks Pdf, Pie Chart DI Data Interpretation Short-Cut Tricks & Tips MCQ, Pie Chart DI Data Interpretation Short-Cut Tricks & Tips Objective Question & Answer Pdf. “Pie Chart DI Data Interpretation Short-Cut Tricks & Tips Questions PDF” In this post we are providing you the Pie Chart DI Data Interpretation Short-Cut Tricks & Tips pdf with detailed solution & Short Tricks. So that you can easily get the logic of question. This Pie Chart DI Data Interpretation Short-Cut Tricks & Tips Pdf we are Providing is free to download. ” Most Important Pie Chart DI Data Interpretation Short-Cut Tricks & Tips Question PDF with Answers“
Pie Chart DI Data Interpretation Short-Cut Tricks & Tips Plays a vital role in Exam. In every exam you will get at least 5-10 questions from this topic. So candidates must focus on this topic and download this Pie Chart DI Data Interpretation Short-Cut Tricks & Tips pdf to get important questions with best solution regarding Pie Chart DI Data Interpretation Short-Cut Tricks & Tips. We have put all Previous Year Questions of Pie Chart DI Data Interpretation Short-Cut Tricks & Tips that are Asked in various Govt & Private Exam.
Pie Charts
They derive their name from its shape, like that of a pie divided into various portions. They always represent data in the form of a percentage of the total, with the total percentage being 100. In such a chart, the length of the arc (and therefore the angle each sector subtends at the centre) is proportional to the quantity it represents. Such charts are often used in the corporate world and in newspapers. Since a circle comprises 360 degrees, each percent of a pie-chart is equal to 360 divided by 100, or 3.6 degrees. This fact will be important for the calculations you are expected to perform.
| Positives | Negatives |
|---|---|
| 1. More effective in calculating the percentage share of each element in the total. | 1. Less accurate than tables as one may take time to establish values. |
| 2. Questions based on comparisons can be effectively solved using pie charts. | 2. Trends cannot be established in a pie-chart. |
| 3. One pie chart can represent only one data set. Hence, when a question pertaining to pie chart is asked, in most cases data pertaining to only one or two data sets are asked. Because of this a student need to handle only limited number of data values. |
4 Tips to Solve Pie Chart Questions
1. Start with the heading.
It tells you exactly what you’re looking at, yet it’s amazing how many students skip the title of the chart and the labels and go straight to the question-stem! Really slow down and examine every tiny piece of writing on and around the pie chart fully before reading the question. What’s the biggest slice? The smallest slice? How many slices total? What does each slice represent? What can be readily inferred? Make sure there isn’t any additional information printed below the chart that may be required to solve.
2. Don’t confuse percents with numbers!
The pie chart may display numbers in each slice (17..19…35, etc.) but these may or may not be percentages. Look for the “%” symbol, or a note somewhere at the bottom of the pie chart that explains what the numbers actually refer to – a percent is always a fraction of 100, while a real-world number is always a fraction of a real-world total.
3. Round numbers up or down to make the math easier.
Just like in other SAT math questions, the answer choices may be far enough apart so that it is somewhat easy to estimate. Rounding to the nearest whole number, percent, or fractional equivalent can sometimes be the simplest way to solve. For example, 47.8% could become 50%, and 69% = 2/3. If you’re pressed for time, approximation can help you eliminate four choices faster than doing the math with the most-accurate values.
4. Don’t forget your knowledge of circles.
Just like in a Geometry question, we can always set up proportions based on part/whole ratios. You might not need to use Circle properties for these Data Analysis questions, but its good knowledge to have up your sleeve! A sector (or “slice”) of a pie chart is always part of the entire area of the pie chart, and an arc of the pie chart is always part of the entire circumference.
Basics:
Total angle at the center of a pie chart = 3600
To convert k% percentage into angle = k100×3600
To convert m0 into percentage = m360×100
Shortcuts to crack DI sets containing Pie Charts
1. Ignore the overall value in comparison based questions and avoid calculating every value.
Here is a CAT 2002 set to illustrate the same.

In the above question, a normal tendency would be to calculate the value and quantity for all 6 suppliers and find out for which country is this ratio the highest. However you need not do this! Since the overall values of both the pie-charts are same for all the countries, we need to simply compare the ratio of the respective percentages of the two pie-charts. This ratio is close to 2 for Switzerland (20 / 11). No other country is even close to this.
2. Replace big values by small values for comparison sake.
Consider this CAT 1999 set for example.

In the first question above, though we can shortlist OPEC (H) and Asia (I) by the sheer value of the percentages, it would take a little while to shortlist between the two. What you could have done is instead of taking the values as $40,779 and $33,979, we could have approximated it as 41 : 34 or approximately 6 : 5. Now, with these values, we can compare H and I easily. For example, in case of H, the total trade would be (23 × 6) + (10 × 5) = 188 and in case of I it would be (14 × 6) + (20 × 5) = 184. Clearly the value is higher for H i.e. OPEC.
3. Deploy smart techniques to do percentage calculations.
Check out this CAT 1995 question.

The above question can be solved in two ways:
Traditional Method: Interest in 1990-91 = 28% of 120 = 33.6, Interest in 1991-92 = 42% of 150 = 63. Hence Percentage increase = 29.4 / 33.6 = 87.5%. Obviously, this would involve some bit of caluculation.
CPLC Method: Overall Operating Profit has increase by 25% i.e. from 120 to 150 (this can be done mentally). The percentage share of interest has increased by 50% i.e. from 28 to 42 (this can be done mentally). Hence, the overall Percentage increase in interest value will be successive percentage of these two values i.e. 25 + 50 + 12.5 = 87.5% (this can be done mentally as well.
What is also means is that if we were required to find that component which has undergone the highest / lowest percentage change over the two years, you can simply find out that component that has undergone the highest / lowest percentage change in its market shares and get the answer. You need not bring the overall values (120 and 150) into the picture at all!
What is a Pie Chart?
A pie chart is a circle which is drawn around an angle of 360 degrees. It is divided into different sectors where each sector represents a particular element, from the given data. A pie chart is useful when percentage proportion of various elements are to be shown. A pie chart is similar to a pizza or a pie, which is cut into four quarters where each quarter represents 25% of the pizza or the pie, likewise, a complete circle is cut into different proportions based on the percentage. A pie chart is visually attractive and helps in making an easy comparison.
In the examination, pie chart questions may contain one, two or three diagrams and have pie chart questions on it. In pie chart questions, we need to take all the pie charts into consideration while solving a problem.
Example of Pie Chart Questions
Problem 1:
Before going ahead let’s look at all the possible questions that can be asked, by taking the accounts department as an example.
- Total number of people in accounts department = 20% of 3600 = 720
- Total number of people who got promoted in accounts department = 8% of 1200 = 96
- Total number of males in account department = 5% of 2040 = 102
- Total number of females in account department = No.of people in accounts department – No.of males in accounts department = 720 -102 = 618
Question 1: If half of the employees who got promoted from IT department are males, what is the approximate percent of males who got promoted from the IT department?
1)61 2)29 3)54 4) 42 5) 38
Solution:
Step 1:
Half of the employees who got promoted from IT departments are males,
Number of people who got promoted from IT department = 26% of 1200 = 312
Number of males who got promoted from IT department = (1/2 ) of 312 = 156
Step 2:
We need to find the percentage of the number of males who got promoted from IT department.
x is what percent of y= x/y x 100 [ Percentage Formula]
x= Number of males who got promoted from IT department = 156
y = Total number of males in IT department = 20% of 2040 = 408
No. of males in IT department/ No. of males x 100
Step 3:
By substituting the values in the formula
156/408 x 100
= 38%
Therefore, the percentage of the number of males who got promoted from the IT department is 38%.
Question 2: What is the total number of females working in the production and marketing department together?
Solution:
Step 1:
We need to find No.of females working in Production and Marketing Department.
No. of female in the Production and Marketing Department = No. of employees in Production and Marketing Dept. – No. of males in Production and Marketing Dept.
Step 2:
We can club departments together instead of finding the number of people working for individual departments.
No.of employee (Production + Marketing) = 3600 (35% + 18%)
= 3600 x 53% = 1908
No.of males (Production + Marketing) = 2040(50% + 15%)
= 65% of 2040 = 1326
No. of females in Production and marketing department = 1908 – 1326
= 582
Therefore, the total number of females in the Production and Marketing Departments are 582.
Question 3: What is the angle made at the centre by the sector showing the number of males in the marketing department?
Solution:
Step 1:
The formula for finding the angle that is made at the centre is,
Percentage of number of males x 360o(As it makes a complete angle)
15% of 360o = 54o
Therefore, the angle that will be made by the total number of males working in the marketing department is 54o.
Question 4: What is the percentage of the total number of people who got promoted from all the departments?
1) 56 2)21 3) 45 4) 33 5) 51
Solution:
Step 1:
As we need to find the percentage change
x is what percent of y = x/y x 100 [Formula]
x -Total number of people who got promoted
in all the departments = 1200
y- Total number of employees in all the departments = 3600
Step 2:
Substituting the values in the formula,
1200 /3600 x 100 = 33.33%
Question 5: What is the ratio of the number of employees who got promoted in HR department to the number of male employees in IT department.
Solution:
Step 1:
We need to find the ratio of,
No. of people promoted in HR department: Number of Males in IT department
Step 2:
By substituting the values in the formulas
11% of 1200: 20% of 2040
Step 3:
By taking percent as common
11 x 1200 : 20 x 2040
11:34
Therefore, The ratio of people who got promoted in HR department and the number of males in IT department is 11:34.
In banking exams we often come across Pie Chart Problems in DI and Quant sections. We can find such problems in IBPS Clerk, SBI Clerk, SSC CGL, IBPS PO, SBI PO, Placement Aptitude and other competitive exams. In these, we are asked to calculate the differences from the values in the given chart.
Sometimes, in Pie Chart problems in DI and Quant, the total value or difference is asked. For these types of questions, no need to calculate individual values from the given chart. You just need to combine the data given in the graph directly and you will find the answer.
Why This Method?
To sit and calculate each value individually could mean the difference between selection and disqualification in the exam. You will waste precious time. Instead use this simple concept to quickly solve Pie chart problems in DI and Quant. If you can’t find the perfect answer, you can even eliminate some options to make an educated guesstimate.
Example of Pie Chart Problems in DI and Quant
Here is an example to understand the basic concept properly.
Directions: Study the following pie-chart carefully to answer these questions.
Percentage-wise Distribution of Players who Play Five Different Sports
Total players = 4200
Ques 1: What is the total number of players who play Football and Rugby together?
1) 620
2) 357
3) 230
4) 630
5) None of these
Ans: 5) None of these
Solution: Total players = 4200
Percentage of players who play football= 17%
Percentage of players who play rugby = 13%
Percentage of players who play both football and rugby = 17% + 13% = 30%
Total players who play football and rugby = 30% of 4200 = 0.3 × 4200 = 1260.
Ques 2: What is the difference between number of players who play Cricket and Lawn Tennis?
1) 360
2) 450
3) 540
4) 420
5) None of these
Ans: 4) 420
Solution: Total players = 4200
Percentage of players who play Cricket = 35%
Percentage of players who play Lawn Tennis = 25%
Difference in Percentage of players who play both Cricket and Lawn Tennis = 35% – 25% = 10%
So, difference in players who play Cricket and Lawn tennis = 10% of 4200 = 420.
Sample Question
Directions: Study the following pie chart and answer the questions that follows:

Total Number of Teachers = 6400
(Uttar Bihar Gramin Bank 2012)
Question 1: If one-thirty sixth of the number of teachers from university F is professors and the salary of each professor is Rs 96000, what will be the total salary of all the professors together from university F?
[1] Rs 307.2 lakh
[2] 32.64 lakh
[3] Rs 3.072 lakh
[4] 3.264 lakh
[5] None of these
Number of teachers from university F = 18% of 6400 = 1152
1/36 of 1152 = 32
Total salary = 32*96000 = 3072000 = 30.72 lakh. Answer [5] is correct. (Note the tricky options [1] and [2])
Question 2: Difference between the total number of teachers in university A, B and C together and the total number of teachers in university D, E and F together is exactly equal to the number of teachers in which university?
[1] A
[2] B
[3] C
[4] D
[5] F
(You don’t even have to calculate the number of teachers. Just presence of mind is needed.)
Number of teachers in university A, B and C = 11+17+19 = 47%
Number of teachers in university D, E and F = 6+29+18 = 53%
Difference = 6% = University D. Answer [4] is correct.
Question 3: What is the average of teachers in university A, C, D and F together?
[1] 854
[2] 3546
[3] 3456
[4] 874
[5] None of these
Again, solving it quickly.
11+19+6+18 = 54%. Average = 54/4 % = [54/400]*6400 = 54*16 = 864. Answer [5] is correct.
Question 4: If twenty five percent of the number of teachers in university C is female, what is the number of male teachers in university C?
[1] 922
[2] 911
[3] 924
[4] 912
[5] None of these
Number of teachers in university C = 19% of 6400 = 19*64 = 1216
25% of this is female. Hence remaining 75% is male.
Number of male teachers = 75% of 1216 = [3/4]*1216 = 912. Option [4] is correct.
Question 5: Number of teachers in university B is approximately what percent of the total number of teachers in university D and E together?
[1] 55%
[2] 59%
[3] 49%
[4] 45%
[5] 65%
Just solve the percentages.
University B = 17%. University D+E = 6+29 = 35%
Required percentage = [17/35]*100 = approx. 49%. Answer is [3]
A pie chart is a circle graph divided into pieces, each displaying the size of some related piece of information. Pie charts are used to display the sizes of parts that make up some whole. In a pie chart, the arc length of each sector (and consequently its central angle and area), is proportional to the quantity it represents. Together, the sectors create a full disk
While the pie chart is perhaps the most ubiquitous statistical chart in the business world and the mass media, it is rarely used in scientific or technical publications. It is one of the most widely criticized charts, and many statisticians recommend to avoid its use altogether. (Source of above paragraph: wikipedia)
Let s first try to put the similar set of data we have used in other charts. Say in CAT07 the number of questions asked from different chapters are
Algebra : 6 Geometry: 9 Number System:12 and Others: 3 and the total number of questions in math section is 30.
So algebra part consist of 6/30 x 100 = 20% of total questions. And similarly
Geometry: 30%
Number System: 40% and
Others: 10%
While representing the above numbers in a pie (circle) we ‘ll allocate the area(and thus the angle) to each section in such a way that each section’s percentage value corresponds to the equivalent area in the pie. And we ll get a chart as shown below.

You must be clear about how to make a pie chart. Now we will do the reverse – try to find information from a given pie chart (which is exactly what you ‘ll be doing in exam)
The below pie chart shows a typical Dhoni’s ODI innings. The numbers shows how many runs he has scored in single , twos, threes , fours and sixes.

After analyzing the above pie chart, try to answer the following questions:
1. What percentage of runs dhoni scored with threes
2. How many runs he had scored with boundaries (Note : both 6 and 4 are considered as boundaries)
3. What is the angle made by the sector representing runs scored in singles?
4. How many 6s he had hit in that innings
From the graph Dhoni has scored 9 runs with threes i.e 3 threes and the total run he has scored in that particular innings is 123.
So the percentage of runs Dhoni scored in 3s is 9/123 x 100 = 7.3%
Answer 2: Total runs scored in boundaries = 54 + 28 = 82
Answer 3: Total runs scored in single is 8 and that is 8/123 x 100 = 6.5% of the total run.
So the angle made is (6.5/100) x 360 = 23.41 degree
Answer 4: Total runs in 6s =54 so number of sixes is 54/6 = 9
Chart Comparison
Pie charts are generally not recommended to visualize information instead use bar- or line chars if the quantities are important.
Studies have shown that pie charts are hard to read if you actually have to answer questions about the numbers they represent. They look very pleasing and are used in a lot of places but they do not help to visualize information that well. Analytic thing person will read the percentages or values given on the legend or the chart it and analyze them in their head.
This is mostly because differences in angles are not easy to judge
For the human eye and there are a bunch of cases were you make the pie chart experience even worse. There are still reasons to use pie charts.
Example 1:

Answer the following questions with reference to the above pie chart
Q1. Of every dollar received by the federal government, how much (in cents) is from coporate sources?
A. 32
B. 70
C. 30
D. 35
E. 29
Answer : 1
Q2. what percentage of the federal revenue is derived from borrowings?
F. 0.2%
G. 0.02%
H. 2.7%
I. 1.2%
J. 2.5%
Answer : 3
Example 2:
Chart 1 shows the distribution of twelve million tonnes of crude oil transport through different modes over a specific period of time. Chart 2 shows the distribution of the cost of transporting this crude oil. The total cost was Rs. 30 million.

1.What is the cost of transporting petroleum by rail (in Rs)?
1. 2.5
2. 3.33
3. 6.4
4. 8
2.If the cost per tonne of transport by ship, air and road are represented by P, Q and R respectively, which of the following is true?
1. R > Q > P
2. P > R > Q
3. P > Q > R
4. R > P > Q
3. The cost in rupees per tonne of oil moved by rails and happens to be roughly
1. 3
2. 1.5
3. 4.5
4. 8
4. From the charts given, it appears that the cheapest mode of transport is:
1. Road
2. Rail
3. Pipeline
4. Ship
5.Which is the most effective way of transportation?
1.Road
2. Ship
3. Pipeline
4. cannot be determined
6.If for some reason ship stop sailing, by what percentage the airfreight have to go up to reach the previous level of volume transported (approximately)?
1. 75%
2. 81%
3. 85%
4 .90%
If the revenue after selling the petroleum was Rs 40 Million and other costs (including oil extraction, marketing etc) is Rs 5 Million, answer the following.
7.What is the Profit percentage?
1. 10%
2. 12.5 %
3. 15%
4. 20%
8. If the cost of transportation rises by 20 % and so does revenue,what is the margin %?
1. 14.08
2. 14.28
3. 14.58
4. 14.78
9.If all costs rise by 10% and revenue remains same ,what would be the decrease in percentage profit?
1. 35
2. 50
3.70 4 .80
10. If the pipeline cost increases by 30% ,by what percentage would revenue have to be increased so as to have same amount of profit?
1. 11.5
2.12.8
3.13.75
4. 14.6
11. If the govt includes a 15% tax on transportation costs ,what would be the effective cost per tonne of petroleum so as to have the same amount of profit as before?
1. 3.2
2.3.5
3.3.7
4. 4.2
1. 2. We get 3.6/1.08=3.33
2. 3 Calculate the cost by ship, air and road.
P = 3/1.08 = 2.77; Q = 2.10/1.32 = 1.58; R = 1.80/2.64 = 0.68 hence P > Q > R
3. 1 3.60/1.08 = 3.33
4. 1 Road is the cheapest, from Q 132.
5. 4 cannot be determined as e do not know on what criteria
6. 2. Air freight is 11% .it would have to increase to 20% i.e. increase by 81.81%
7. 2. 12.5 %
8. 3. 14.58 profit of 7 Million on revenue of 48 Million
9. 3. 70 %
10.4. Pipeline cost is 65%ie 19.5 Million. If this rises by 30 %, it rises by 5.85 Million .to offset this, Revenue would have to rise by the same amount, so 100 = 14.625%
11. 3. 3.7
Example 3:

Answer the following questions with reference to the above pie chart
Q1. What fraction of Ghosh babu’s weight consists of muscular and skin proteins?
(a) 1/13
(b) 1/30
(c) 1/20
(d) Cannot be determined
Q2. Ratio of distribution of protein in muscle to the distribution of protein in skin is:
(a) 3 : 1
(b) 3 : 10
(c) 1 : 3
(d) 3(1/2): 1
Q3. What percent of Ghosh babu’s body weight is made up of skin?
(a)0.15
(b) 10
(c) 1.2
(d) Cannot be determined
Q4. In terms of total body weight, the portion of material other than water and protein is
closest to:
(a)3/20
(b)1/15
(c)85/100
(d) 1/20
ANSWERS 1.(c) 2.(a) 3.(d) 4.(a)
Example 4:
The following pie charts give the percentage distribution of different types of employees in different departments, A, B, C, D and E.

1. What was the difference in total number of people in department A in 1999 and 2000?
(1)840
(2) 400
(3) 440
(4) 240
2. In the case of which department was there a maximum variation between 1999 and 2000?
(1)E
(2)B
(3)D
(4) A
3. If 300 employees left in department B at the end of 1999, how many people joined in this department in 2000?
(1) 340
(2) 460 (3) 980
(4) 1360
4. The number of employees in department D in 2000 is how many times the number of employees in department E in 1999?
(1) 3.5
(2) 2.8
(3) 2.33
(4) 1.77
5. What is the percentage increase in the number of employees in department C in 1999- 2000?
(1) 2%
(2) 2.34%
(3) 23.45%
(4) None of these
6. If the average monthly salary of employees in department A in 1999 was Rs 4,000, what was the annual salary bill for department A in 1999?
(1) Rs 19 lakh
(2) Rs 19 crore
(3) Rs 22 crore
(4) Rs 22 lakh
7. If the average salary for the whole company remained same in 1999 and 2000 at the level of Rs.5,000 per month, what was the percentage increase in the salary bill for the company in the two years?
(1) 4%
(2) 8%
(3) 9%
(4) 11%
ANSWERS:
1. 1 22% (18000) – 24% (20,000)
2. 3 Visually, we see D has the maximum variation.
3. 4 26% (20,000) = 23% (18,000) + 300
4. 2 20% (20,000)/8% (18,000)
5. 3 18% (18,000) to 20% (20,000) = 23.45%
6. 2 22% (18,000) ï€¿ï€ 4000.
7. 4 (20 – 18)/18 = 11%
Set 1 : The various sections of the population are indicated below in the pie-chart. Study the pie-chart and answer the following questions:
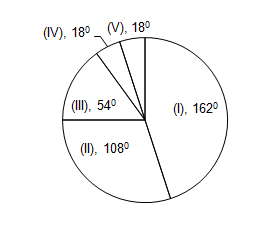
I. Employees of the Public Sector II. Employees of the Private Sector
III. Employees of the Corporate Sector IV. Self-Employed V. Unemployed.
1. What percentage of the employed persons is self employed?
| a. 5% | b. 5 5/19 % | c. 19% | d. 20% |
Solution: Total Employed = Total population – Unemployed = 3600−180=3420
Now self employed are 180. So self employed as a percentage of employed = 18342×100=5519%
2. Number of persons employed in the Corporate Sector is
| a. 250 | b. 500 | c. 750 | d. 1500 |
Solution: We have to convert degrees into numbers. So 54360×5000=750
3. The number of Unemployed persons is
| a. 250 | b. 150 | c. 100 | d. 50 |
Solution: We have to convert degrees into numbers. So 18360×5000=250
Shortcut: We calculated corporate sector employees as 750. But from pie chart Corporate sector employees are 3 times of unemployed. So 1/3rd of 750 = 250
4. The number of persons employed in both the Public Sector and Corporate Sector is
| a. 3750 | b. 3000 | c. 2500 | d. 2200 |
Solution: Number of persons employed in public sector and corporate sector together = 54 + 162 = 216.
54+162360×5000=216360×5000=3000
5. What percentage of the employed persons is employed in Private Sector ?
| a. 29% | b. 31 11/19% | c. 34% | d. 31% |
From the 1st question, employed are 342. and From pie chart private sector employees are 108.
108342×100=60019=311119%
Set 2: These questions are based on following graphs Classification of appeared candidates in a competitive test from different states and qualified candidates from those states.
1. What is the ratio between the number of appeared candidates from states C and E together and the appeared candidates from states A and F together ?
a. 17 : 33
b. 11 : 13
c. 13 : 27
d. 17 : 27
Solution: There is not need to calculate values. This is simply a ratio. So we can compare the ratio of their percentages. C + E = 8 + 9 = 17; A + F = 15 + 18 = 33.
So ratio = 17 : 33
2. In which State the percentage of qualified candidates to that of appeared candidates is minimum ?
Solution: This is a lengthy question. But we will use simple technique to solve this question.
We have to calculate the ratio of Qualified to appeared for each state. So
But If you observe in the above equation, only 18% / 15% changes for each state. Remaining values are constant. Minimum percentage we get if numerator is small and denominator is big.
For C it is 7/8 = 1/1.14 and for E it is 9/14 = 1/1.5 So for E denominator is big. So it has the ratio Minimum.
So Option D is correct.3. What is the difference between the number of qualified candidates of states D and G
| a. 690 | b. 670 | c. 780 | d. 720 |
Solution: Instead of calculating qualified candidates for D and G separately, we take the difference in their percentages. i.e., 8% (9000) = 720.
4. What is the percentage of qualified candidates to that of appeared candidates from states B and C taken together ?
| a. 23.11 | b. 24.21 | c. 21.24 | d. 23 |
Qualified candidates from B and C = (16 + 7)% = 23% (9000)
Appeared candidates from B and C = (11 + 8)% = 19% (45000)
So required percentage =
23%(9000)19%(45000)×100=2319×5×100=24.21
5. What is the ratio between number of candidates qualified from states B and D together and the number of candidates appeared from state C respectively ?
| a. 8 : 37 | b. 11 : 12 | c. 37 : 48 | d. 7 : 37 |
Solution: The required ration = (16 + 21)% (9000) : 8% (45000)
Example 1
Consider the information provided in the pie chart below relating to India’s foreign trade in 1997-98 and the first eight months of 1998-99. Total trade with a region is defined as the sum of exports to and imports from that region.
Trade deficit is defined as the excess of imports over exports. Trade deficit may be negative.

Example 1.A
What is the region with which India had highest total trade in 1997-98?
(A) USA (B) Other E.U. (C) OPEC (D) Others
Answer – (C)
Solution:
Trade with a region is the aggregate of imports from and exports to that region. The question is about a relative position and not an absolute position and thus should involve nothing more than glancing the pie charts and at the very most some small additions that can eminently he done orally. Whatever he the figures of total exports and total imports, these will not be necessary since what is asked is a relative position.
If we assume that the total exports is E and total imports is I, then in the case of USA, the imports will be 9I1009I100 and exports will be 19E10019E100 and in the case of Other E.U. imports will be 12I10012I100 and exports will be 14E10014E100. So when you are comparing (9I100+19E100)(9I100+19E100) with (12I100+14E100)(12I100+14E100), you can safely multiply both sides so as to get whole numbers such that now we shall be comparing (9I+19E)(9I+19E) with (12I+14E)(12I+14E).
In the present case, imports into India are USD 40779 million and we may safely take I as 4 (rounding off 40779 to the nearest ten thousand) and exports from India are USD 33979 million we may safely take E as 3 (rounding off 33979 to the nearest ten thousand).
Comparing (9I+19E)(9I+19E) with (12I+14E)(12I+14E) will mean comparing (9∗4+19∗3)(9∗4+19∗3) with (12∗4+14∗3)(12∗4+14∗3) and hence 93 with 90 and so India’s total trade with USA is more than the total trade with Other EUs. In evaluating the options, all that one has to do is to put the percentage of imports and if it is say 21% then write it as 21 and write the imports as 4 and so on. Now see the Options.
Option A: USA (9∗4+19∗3)=93(9∗4+19∗3)=93
Option B: Other EU (12∗4+14∗3)=90(12∗4+14∗3)=90
Option C: OPEC (23∗4+10∗3)=122(23∗4+10∗3)=122
Option D: Others (1∗4+1∗3)=7(1∗4+1∗3)=7
Option C is the clear choice. It would be stupid to merely add the percentages alone. A percentage is after all so much out of the whole. If you are comparing percentages of the same whole, you can tell which is higher. But comparing differing percentages of two different wholes is logical only when you take their absolute values. For Example 9% of 200 (we shall call 200 as A) is far higher than 36% of 40 (we shall call 40 as B) and rushing to the conclusion that 36% of B is higher than 9% of A would be stupid.
Assuming 40779 as 4 and 33979 as 3 would:
(A) Save a lot of time.
(B) Save a lot of effort..
(C) Ensure that we are comparing equals on both sides, and
(D) Ensure that you get the correct answer in a jiffy.
Example 1.B
In 1997-98 the amount of Indian exports, in millions US $, to the region with which India had the lowest total trade, is approximately:
(A) 750 (B) 340 (C) 220 (D) 440
Answer – (B)
Solution
Others occupy 1% of the pie in both imports and exports and is the area with the lowest total trade. Indian exports aggregate roughly 34000 million and 1% of this is two zeroes off from 34000 and would mean 340. Thus Option B.
Example 1.C
In I997-98, the trade deficit with respect to India, in billions of US $, for the region with the highest trade deficit with respect to India, is approximately equal to:
(A) 6.0 (B) 3.0 (C) 4.5 (D) 7.5
Answer – (A)
Solution:
Let us assume that total imports are 100I and total exports are 100E. In case of one region – Region 1 – the imports are A% and exports are B% and in region 2 imports are C% and exports are D%. Trade deficit in Region 1 is (AI−BE)(AI−BE) and in Region 2 it is (CI−DE)(CI−DE).
If Trade deficit in Region 1 is higher than in Region 2, then (AI−BE)−(CI−DE)(AI−BE)−(CI−DE) should yield a positive difference and this means that (AI−BE)>(CI−DE)(AI−BE)>(CI−DE). If you subtract CICI to both sides and add BEBE to both sides, you would get:
(AI−CI)>(BE−DE)(AI−CI)>(BE−DE) or I(A−C)>E(B−D)I(A−C)>E(B−D).
We know that I is greater than E in any case.
If (A−C)(A−C) is greater than (B−D)(B−D) the matter is clinched because then I(A−C)I(A−C) is indeed > E(B−D)E(B−D) and thus Trade deficit in Region 1> Trade deficit in Region 2.’
After all, (A−C)(A−C) is some number and (B−D)(B−D) is some other number. So (A−C)%(A−C)% of a higher base is bound to be higher than (B−D)%(B−D)% of a lower base so long as (A−C)>(B−D)(A−C)>(B−D). This is utter logic. This logic is what is at test here.
In the present case, in all regions except OPEC and other East Europe, exports percentages are either more than or equal to imports percentages. We have to thus compare only OPEC and other East Europe and see whether (Difference in percentages of imports)> (Difference in percentages of exports).
In the case of OPEC and other East Europe (Difference in percentages of imports)=(23−19)(23−19) and (Difference in percentages of exports)=(10−10)(10−10) and hence (Difference in percentages of imports)>(Difference in percentages of exports) and thus trade deficit in OPEC is highest.
The trade deficit in this case works out to (0.23∗41−0.1∗34)=9.2−3.4=5.8(0.23∗41−0.1∗34)=9.2−3.4=5.8 roughly.
Thus Option A: 6 billion.
Example 1.D
What is the region with the lowest trade deficit with India in 1997 – 98?
(A) USA (B) Asia (C) Others (D) Other E.U.
Answer – (A)
Solution:
The lowest trade deficit can also means a negative trade deficit or trade surplus. In case of the earlier question we have seen that Other EU has the second highest trade deficit and thus it is not a likely candidate for the least trade deficit. Hence we cross out Option D.
In USA and Asia we have trade surplus. In case of others there is a deficit. When we have trade surpluses, then we are to ignore trade deficits because a trade surplus is a negative trade deficit. So Option C is to be crossed out as well. We are now left with Options 1 and 2.
As we have seen in the earlier question, if (Difference in percentages of imports) is greater than (Difference in percentages of exports) than Trade deficit in Region 1 > Trade deficit in Region 2. Now if we are to compare USA with Asia,
(Difference in percentages of imports) =(9−14)=−5=(9−14)=−5 and
(Difference in percentages of exports)=(19−20)=−1=(19−20)=−1.
Since -5 is not higher than -1, the trade deficit in USA is lower than the trade deficit in the case of Asia and hence Option A.
ADDITIONAL DIRECTIONS for Examples 1.E and 1.F: Those questions are based on the situation below:
Assume that the average monthly exports from India and imports to India during the remaining four months of 1998-99 would be the same as that for the first eight months of the year.
Example 1.E
What is the region to which Indian imports registered the highest percentage growth between 1997-98 and 1998-99?
(A) Other East Europe (B) USA (C) Asia (D) Exports have declined, no growth
Answer – (B)
Solution:
Look at the pie chart for exports in 1997-98, which is for a full year and for 1998 99, which is for eight months only.
As per the additional information, we are to assume that the average monthly exports from India and imports to India during the remaining four months of 1998-99 would be the same as that for the first eight months of the year.
If for eight months, the total exports have been 21436 million, the remaining four months (which is half of eight months) would have brought about an additional export equal to half of 21436 million, which is 10718 and the total exports would then have been 32154 million.
Since we are to state a comparative position – growth rate in exports in 1997-98 and exports in 1998-99, we can safely ignore the millions.
11% of 100 is less than 9% of 200 and so also 11% of I00 Billion is less than 9% of 200 Billion. What is the need for these millions while stating which is greater?
Secondly, if you are to compare between growth in exports over base yeah then you must appreciate that exports in 1998-99= exports in 1997-98 + growth in between/exports in 1997-98 = 1+ growth in between/exports in 1997-98 and thus when you compare the exports of two different regions, you can safely take the exports in the next year as a fraction of the base year instead of finding the difference between the exports in an year and the exports in the base year because when you compare the exports figures of Region 1 with that of Region 2 instead of incremental exports, you will get 1 on both sides of the comparison like this:
[1+ growth in between of exports in Region 1/exports in 1997-98] compared with [1+ growth in between of exports in Region 2/ exports in 1997-98], and if you strike off the 1 on both sides what you are really comparing is:
[Growth in between of exports in Region 1/exports in 1997-98] with [Growth in between of exports in Region 2/exports in 1997-98] which is what you want.
Let us see the options.
Option A:
Other East Europe. 10% of 33979 has grown to 12% of 32154. Let 1% of 33979 be A and 1% of 32154 be B. So in the case of Other East Europe, exports in 1998-99/exports in 1997-98 = 12B/10A.
Option B:
USA, 19% of 33979 has grown to 23% of 32154. Let 1% of 33979 be A and 1% of 32154 be B. So in the case of USA, exports in 1998-99/exports in 1997-98 = 23B/19A.
Option C:
Asia, 20% of 33979 has grown to 19% of 32154. Let 1% of 33979 be A and 1% of 32154 be B. So in the case of Asia, exports in 1998-99/exports in 1997-98 = 18B/20A.
Now what we are required to do is to compare among 12B/10A, 23B/19A and 18B/20A and say which is largest. In that case, neither B nor A in the numerator and denominator respectively are necessary because if you multiply all three fractions by A/B then you get 12/10, 23/19 and 18/20 and yet the relative values of the three fractious will remain unchanged.
If you were to multiply three fractions – say – 1/2, 2/3, and 3/4 by one million in the numerator and five million in the denominator, will it alter the fact that 3/4 (as it will seem after all the multiplications) will remain the largest and 1/2 the smallest of these three fractions? See for yourself. The three fractions will respectively seem like this: 1 million/10 million, 2 million/15 million and 3 million/20 million and yet the last will be the highest and the first will be the lowest.
So what you are then comparing is 12/10, 23/19 and 18/20 in which 18/20 will have to be booted out since it is less than 1 and then we are left with 12/10 and 23/19. If we divide 12 by 10, we get 1.2.
If we divide 23/19 we get 1.2 till the first decimal and have to carry on to the next decimal and hence we get 1.21. We stop here and declare that USA has highest growth among the three options and thus Option B is correct.
But there is a small googly here. Option D says that exports have declined or there has been no growth in any region. This has to be checked. We know that the highest percentage growth is in the case of USA. But percentage growth is about relative growth whereas the Option D talks about absolute growth. Whether there has been no growth or decline in absolute terms can be ascertained from only absolute figures.
Now see the utter logic in this. If this logic goes home, you will be saved a huge lot of calculations. Logic is the name of the game and even if it takes some time for this simple logic to register, it is recommended that you should absorb the fundamentals.
Since we know that in case of USA the percentage growth rate has been highest, we may just see whether there has been actual growth in this case (we shall choose the highest percentage growth rate to check because if there has not been absolute growth where the percentage growth is highest, then in cases of lower percentage growth, the likelihood of an absolute growth is zero).
In case of USA, export percentage grew from 19% of 33979 million to 23% of 32154 million. For determining whether there was growth, the millions are unnecessary once again. They would be needed if you were asked how much was the growth.
But even then, if the answer is to be given in millions, the millions become redundant once again. Give these millions a well-earned rest. Round off 33979 to 34 (forget the thousands as well) and round off 32154 to 32 (forget the thousands here as well) and see whether 19% of 34 is less than 23% of 32. You will find that so exports have indeed grown in the case of USA at least and hence Option D (which if true would mean that there has not been any growth in exports in any region) does not hold water.
So Option B.
Example 1.F
What is the percentage growth rate in India’s total trade deficit between 1997-98 and1998-99?
(A) 43% (B) 47% (C) 50% (D) 40%
Answer – (B)
Solution:
lndia’s trade deficit in 1997-98 in USD billions is:
40.7−33.9=6.840.7−33.9=6.8
In 1998-99, it is (28.1∗1.5)−(21.4∗1.5)=42.15−32.1=10.05(28.1∗1.5)−(21.4∗1.5)=42.15−32.1=10.05.
The trade deficit has gone up from 6.8 billion USD by 3.25 billion USD to 10.05.
This increase of 3.25 as a percentage of 6.8 is:
3.25∗1006.8=3256.83.25∗1006.8=3256.8
=325068=162534=325068=162534.
Now 34∗50=170034∗50=1700. 1625 is 75 less than 1700.
So 162534=50−(7534)162534=50−(7534).
But 75347534 is more than 2 and thus 162534162534 is likely to be more than 47 and less than 48.
From among the options 47% seems to be the answer. So Option B: 47%.










